MATLAB

El nombre MatLab es una abreviatura de las palabras MATrix LABoratory. MatLab es un sistema interactivo para cálculos científicos y de ingeniería basado en las matrices. Con el se pueden resolver complejos problemas numéricos sin necesidad de escribir un programa específico para ello, aunque también es posible programar. Además, el programa MATLAB dispone, dependiendo de la versión, de diferentes módulos (Toolboxes) que permiten resolver problemas específicos.

1. MANEJO ELEMENTAL DE MATLAB

Iniciando el programa.

En Matlab, las ordenes se introducen escribiéndolas una a una a continuación del prompt (>>) también se le puede decir apuntador, que se presenta en la ventana del usuario.

Veamos en primer lugar, algunas de las operaciones matemáticas más elementales.

Para sumar dos números:

>>2+2

ans =

Después de escribir cada comando hay que pulsar Intro (ENTER) para que lo ejecute. Si después de esta agotadora primera sesión con MatLab queremos salir del programa, se puede hacer de dos formas, escribiendo exit a continuación del prompt, o bien con:

File Exit MATLAB.

El valor que queremos calcular también se puede asignar a una variable. Por ejemplo:

x=3^2

y=9

Hay que tener en cuenta que MatLab distingue entre mayúsculas y minúsculas, por lo tanto, se distingue entre la variable X y la variable x.

La notación para las operaciones matemáticas elementales es la habitual en todos los programas de Calculo Simbólico:

Suma +

Resta -

División /

Exponenciación (potencia) ^

Multiplicación *

También están definidas algunas de las funciones más comunes utilizadas en Matemáticas. Su sintaxis coincide también con la que se utiliza en la mayoría de los programas de Matemáticas, como, por ejemplo, el programa DERIVE, aunque hay algunas diferencias. Algunas de estas funciones son:

sin	seno
sinh	seno hiperbólico
asin	arco seno
cos	coseno
cosh	coseno hiperbólico
acos	arco coseno
tan	tangente
atan	arco tangente
exp	exponencial
log	logaritmo neperiano
log10	logaritmo decimal
sqrt	raíz cuadrada
abs	valor absoluto

Si conocemos el nombre del comando, pero queremos saber para qué sirve, se puede poner:

>>help comando

Interfaz de usuario. Variables

Con las flechas del cursor, se pueden recuperar las órdenes anteriores, sin tener que volver a teclearlas. Esto resulta útil en el caso de una equivocación o cuando se quiere repetir un comando con alguna pequeña modificación.

A veces, puede resultar necesario, hasta imprescindible, que el resultado de un cálculo no se presente en pantalla. Por ejemplo, si generamos una matriz de orden muy alto con el objeto de hacer después una gráfica.

El hecho de que se presente la matriz en pantalla puede resultar un poco engorroso. Para conseguir esto se pone un punto y coma al final de la instrucción.

Por ejemplo,

x=sin(3); % el resultado siempre está en radianes

No se percibe ningún resultado, pero ha realizado el cálculo, porque si escribimos el valor de x, mostrara el valor 0.1411.

Los comandos se pueden ir escribiendo y ejecutando uno a uno, es decir, renglón a renglón, y también se pueden escribir uno a continuación de otro en una misma línea, en cuyo caso deben ir separados por comas.

Si el comando o la cantidad de comandos son demasiado largos para que aparezca en un único renglón, se puede romper la cadena y seguir en el siguiente renglón, escribiendo tres puntos suspensivos. Por ejemplo,

>>x=sin(10),y=cos(10),...

z=tan(10)

x =

-0.5440

y =

-0.8391

z =

0.6484

Los resultados numéricos que ofrece MatLab se pueden visualizar en diferentes formatos. Por defecto, si un resultado es un número entero, lo ofrecerá como tal. Si no lo es, lo haría con 4 cifras decimales (redondeando a la cuarta cifra). Si el resultado es un número grande, lo expresara en notación científica. Este formato que usa por defecto se puede modificar en el menú File Preferences Numeric Format, aunque también se puede hacer directamente escribiendo las órdenes a continuación

>>:

Si escribimos:

>>x=34/8449;

Y ahora iremos cambiando el formato como se indica en la siguiente tabla, volviendo a escribir >>x, cada vez se obtiene el mismo resultado en las distintas formas numéricas.

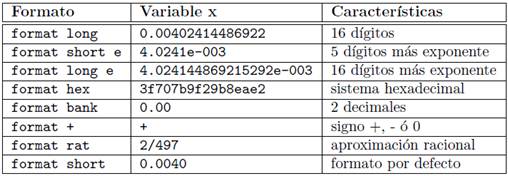
No obstante, independientemente del formato que se esté utilizando, la representación interna del número siempre es la misma, lo único que cambia es la forma en que lo vemos en la pantalla.

En Matlab, lo normal es ir asignando valores escalares o matriciales a variables, si en un momento determinado queremos saber con qué variables estamos trabajando, se puede escribir >>who, que nos indica que variables están en uso; el comando >>whos, nos indica lo mismo, pero además nos informa del tamaño y del tipo de variable. O bien, en el ítem File con Show Workspace, que produce el mismo resultado que >>whos. Para borrar una variable, se puede utilizar el comando >>clear variable, y borrara la variable que se indique, si se pone solo >>clear, se borraran todas las variables que se estén utilizando actualmente.

Las variables pueden contener hasta 19 caracteres, los caracteres más allá del 19 se ignoran. Las variables deben comenzar con una letra, seguida por letras, dígitos o guiones de subrayado.

Además hay algunas variables especiales que se utilizan por defecto: ans: Es la variable que se utiliza en los resultados. En la operación siguiente se puede recuperar este resultado volviendo a escribir ans. Esta variable se modificara en cuanto haya un nuevo resultado.

pi: El número (No hay una variable para el numero e pero se podría definir >>e=exp(1)).

eps: Es el número más pequeño que utiliza el ordenador tal que, cuando se le suma 1, crea un número en coma flotante mayor que 1.

Inf: Infinito, se presenta si hacemos 1=0.

NaN: Mensaje de error (Not a Number), por ejemplo, 0=0.

realmin, realmax: Son, respectivamente, el menor y el mayor de los números reales utilizables.

Vectores y matrices

Los vectores y las matrices son los elementos básicos con los que trabaja Matlab. Veamos cómo se introducen y como se pueden hacer algunas de las operaciones elementales con ellos.

Poniendo el símbolo % se consigue que no se ejecute lo que venga a continuación, en el mismo renglón, sino que se interprete como un comentario, se suele utilizar para escribir comentarios aclaratorios en líneas de comandos de manera que no afecten a su ejecución. Por ejemplo, si ponemos, >>sqrt(2) % Raíz cuadrada de 2 calculara la raíz de 2 y se saltara el comentario.

VECTORES. Un vector se puede definir introduciendo sus coordenadas, separadas por espacios o por comas, entre corchetes:

>> x=[1 2 3]

x = 1 2 3

Si queremos definir un vector columna, se separan las filas por puntos y comas, o bien se calcula el transpuesto de un vector fila con >>x'.

Otra forma de crear vectores es la siguiente:

>> x=1:0.5:3

x = 1.0000 1.5000 2.0000 2.5000 3.0000

Que genera un vector que va desde 1 hasta 3 con un paso (incremento) de 0.5 unidades.

Exactamente el mismo resultado lo conseguiremos con el comando linspace

>>x=linspace(1,3,5)

Que produce 5 números igualmente espaciados entre 1 y 3.

PRODUCTO ESCALAR. Consideremos los dos vectores siguientes:

>>a=[1 2 3];b=[2 -3 5];

Si los multiplicamos de la forma

c=a.*b

c =

2 -6 15

Obtenemos el producto de los elementos del primero y del segundo vector elemento a elemento. Para obtener el valor del producto escalar

>>sum(c)

ans =11

El producto de dos vectores o dos matrices elemento a elemento sería muy importante cuando queramos representar graficas de funciones.

MATRICES. Para introducir una matriz, se separa cada fila con un punto y coma

A=[3 2 1; 6 5 4; 9 8 7]

A =

3 2 1

6 5 4

9 8 7

Ejercicio 1. Después de definida la matriz, probar los siguientes comandos e intentar descubrir para que sirven:

X=[0.5 0.3 0.2 0.8 0.4 -0.2];

Y=[0.8 0.2 -0.6 -0.3 0.9 0.1];

Z=X*Y

Z=X.*Y

MATRICES PREDEFINIDAS.

En MatLab hay varios comandos que sirven para definir con gran facilidad matrices de tipos particulares. Algunas de estas funciones son las siguientes:

eye(n), matriz unidad de tamaño (n x n)

zeros(m,n), matriz de ceros de tamano (m x n)

zeros(n), lo mismo, pero de orden (n x n)

ones(n), matriz de unos (n x n)

ones(m,n), lo mismo, pero de orden (m x n)

linspace(x1,x2,n), genera un vector con n valores igualmente espaciados entre x1 y x2

logspace(d1,d2,n), genera un vector con n valores espaciados logarítmicamente entre 10^d1 y 10^d2

rand(n), matriz de números aleatorios entre 0 y 1, distribuidos uniformemente (n x n)

rand(m,n), lo mismo, de tamaño m x n

randn(n), matriz de números aleatorios (nxn), distribuidos según la normal estándar, N(0; 1)

magic(n), crea una matriz en forma de cuadrado mágico de tamaño n x n

EJERCICIOS ARITMETICOS PASARLOS A MATLAB:

ARITMETICO MATLAB RESULTADO ESPERADO

7 + 8/2                               7+(8/2)                                     11
7+8 / 2                              (7+8) / 2                                   7.5000
4+ 5/3 +1                           4+(5/3) +1                                6.6667
5³ /2                                   (5^3)/2                                    62.5000

Las siguentes ecuaciones aritmeticas pasarlas a MATLAB Y VERIFICAR CON SU RESULTADO

RESULTADO ESPERADO

9.5917

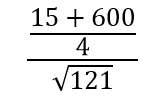
13.9773

Lenguaje simbolico

El Toolbox de Matemática Simbólica, añade a MATLAB la capacidad de realizar cálculos simbólicos basados en MAPLE V © soportando además (The Extended Symbolic Math Toolbox) las librerías especializadas, y los programas realizados para este último. Entre otros, los principales tipos de operaciones soportados son los siguientes:

Algebra simbólica: Derivación, integración y simplificación de expresiones matemáticas.

Algebra lineal exacta: Inversas, determinantes, auto valores y formas canónicas de matrices simbólicas.

Aritmética de precisión variable: Evaluación de expresiones matemáticas con diversos grados de precisión.

Resolución de ecuaciones: Resolución numérica y simbólica de ecuaciones algebraicas y diferenciales.

Funciones matemáticas especiales: Evaluación de la mayoría de las funciones utilizadas en matemáticas aplicadas.

Existen dos versiones del mismo Toolbox. The Basic Symbolic Math Toolbox es una colección de más de 50 funciones MATLAB las cuales permiten acceder al kernel de MAPLE utilizando la Sintaxis y el estilo del lenguaje MATLAB. The Extended Symbolic Math Toolbox aumenta esta funcionalidad incluyendo todas las características de programación de MAPLE, y el acceso a los paquetes de funciones de más de veinte campos de las matemáticas especiales aplicadas.

Es posible utilizar este Toolbox sin conocimiento previo de MAPLE, ya que los ficheros contenidos en él son totalmente autónomos. Sin embargo, si lo que se desea es obtener toda la potencia de cálculo del entorno, será necesario un amplio conocimiento del manejo y la programación de MAPLE

Ejemplo de lenguaje simbólico

Las variables simbólicas.- es una variable cuyo valor, no es un número, sino una expresión o una letra.

a=sym('a');

b=sym('b');

x=sym('x');

f=sym('3*x^3+a*x+b');

>>f=sym('(3*x^2-2)^2');

>>f1=expand(f); % desarrolla la ecuación de forma algebraica

>>ezplot(f1) % la gráfica la ecuación anterior

También es posible graficar con:

>>fplot('x^2',[0,4]) % grafica la ecuación x^2 del intervalo 0 a 4

2. GRAFICAS 2D

Funciones de la forma y = f(x)

Para hacer graficas de funciones de una variable con MatLab, primero tenemos que crear una tabla de valores de la variable para después dibujar la función. Por ejemplo, queremos dibujar la gráfica de la función y = sen(x):

Primero creamos una tabla de valores para x >>x=0:pi/100:2*pi;

Con este comando hemos formado una tabla (el vector x) con 200 valores entre 0 y 2*π. Otra forma de conseguir el mismo resultado sería utilizar el comando:

>>x=linspace(0,2*pi,200);

Ahora calculamos los valores de y escribinos lo siguente: >> y = sin(x);

y por último la dibujamos

>>plot(x,y)

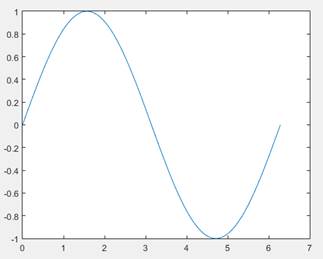
Realmente lo que hemos hecho es dibujar 200 puntos de la función en el intervalo [0; 2*π], y posteriormente el programa los ha unido mediante segmentos. Si el número de puntos es lo suficientemente grande, como en este caso, no se aprecian los vértices.

Veamos un ejemplo algo más complicado. Queremos dibujar ahora la gráfica de la función y = xe^-x2

Definimos los valores para los que queremos hacer la grafica

>>x=-3:.01:3;

Es decir, que vamos a dibujar la gráfica en el intervalo [-3; 3] con un paso de longitud 0.01.

Definimos la función

>>y=x.*exp(-x.^2);

(Por que hay que poner los puntos antes de las operaciones?)

Y por último, se escribe el comando para que ejecute el dibujo

>>plot(x,y)

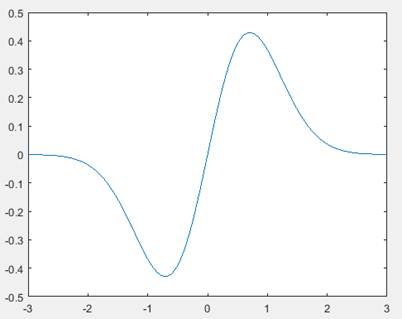
El aspecto de la gráfica se puede modificar utilizando algunos comandos:

- Cuadricula. Si queremos una cuadrícula sobre el dibujo, utilizaremos el comando >>grid on. El aspecto del dibujo será ahora como el de la figura. Para desactivar la cuadricula habría que escribir >>grid off.

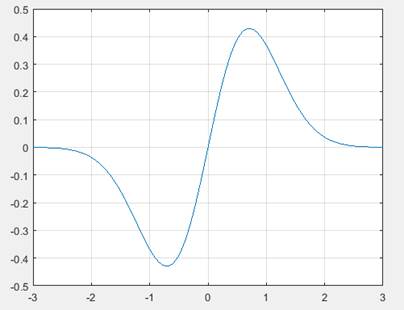
- Color y trazo. El comando plot ofrece múltiples posibilidades de color y forma de trazo de la gráfica. Por ejemplo, el comando >>plot(x,y,'r*'), nos dibujaría la gráfica en color rojo y con asteriscos. Para consultar todas las posibilidades, hacer >>help plot.

Repitiendo el último ejercicio pero con una pequeña variante:

>>x=-3:0.1:3;

Es decir, que vamos a dibujar la gráfica en el intervalo [-3; 3] con un paso de longitud 0.1.

Definimos la función

>>y=x.*exp(-x.^2);

>>plot(x,y,'r*')

>>grid on

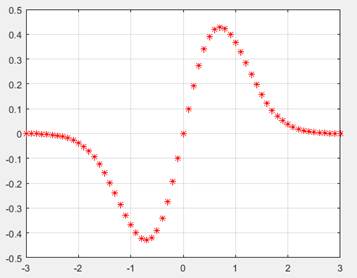
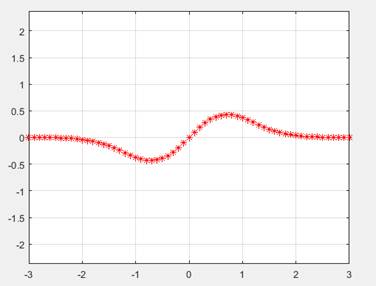
- Ejes. Los ejes por defecto en una gráfica también se pueden modificar. Con el comando >>axis([-2 2 -1 1]), conseguiremos que la gráfica en la región, esto significa el el valor de x sera del rango de -2 hasta +2, y de -1 hasta +1.

Con >>axis square, conseguiremos que la figura en un cuadrado, sin cambiar el rango de los ejes. Con el comando >>axis equal, conseguiremos que los rangos de los ejes sean iguales.

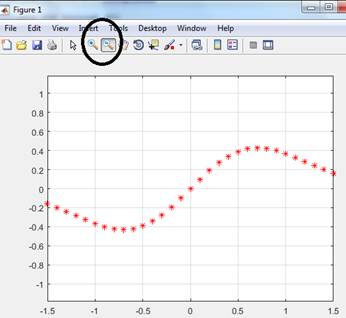
- Zoom. Utilizando el comando >>zoom on. Se puede agrandar la figura o alguna zona seleccionada de la figura. Hay que abrir la figura y utilizar los botones izquierdos y derecho del ratón. Para desactivarlo, habrá que escribir >>zoom off.

- Varias graficas en la misma figura. Se pueden dibujar tantas graficas como se quieran en una misma figura. Si ya tenemos dibujada una, y generamos una nueva gráfica, en principio la figura anterior es sustituida por la nueva. Sin embargo, utilizando el comando >>hold on, se mantendrá la anterior, con todas sus propiedades, y se podrá dibujar encima una nueva. Para desactivar el comando anterior: >>hold off.

Otra forma de hacerlo es dibujar desde el principio dos graficas juntas, por ejemplo, vamos a dibujar las gráficas de las funciones y = sen(x) e y = sen(x +π/3) en la misma figura.

Generamos las tablas:

>>x=linspace(0,2*pi,300);

>>y=sin(x);

>>z=sin(x+pi/3);

Y ahora las dibujamos con:

>>plot(x,y,'r-',x,z,'g--'),grid on

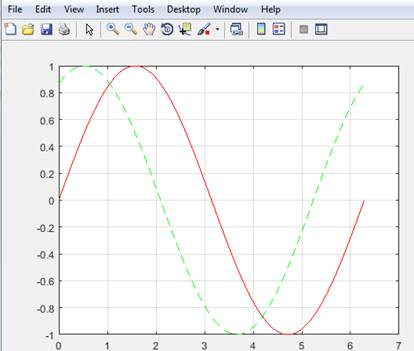
(La primera en color rojo, con trazo continuo, y la segunda en verde, con trazo discontinuo).

- Etiquetado de gráficas. Existen diversas posibilidades para el etiquetado de las gráficas. Veámoslo con un ejemplo:

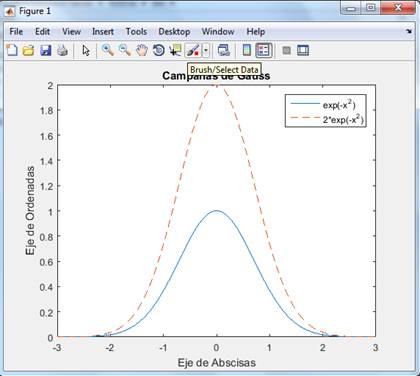
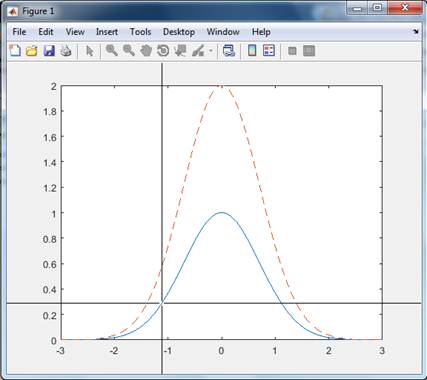
>>x=linspace(-3,3,500);y=exp(-x.^2);z=2*exp(-x.^2);

>>plot(x,y,'-',x,z,'--') % dibujamos dos funciones

>>title('Campanas de Gauss')

>>xlabel('Eje de Abscisas') % Etiqueta el eje horizontal

>>ylabel('Eje de Ordenadas') % Etiqueta el eje vertical

>>legend('exp(-x^2)', '2*exp(-x^2)') % Pone una leyenda

(nota: el simbolo % es para realizar un comentario en la linea no tiene efecto lo escrito despues del %)

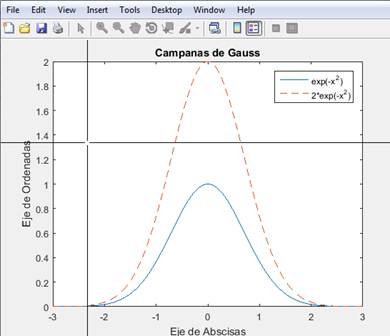
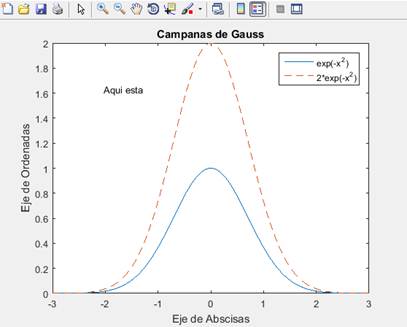
Además de los comandos descritos antes para etiquetar graficas, existe la posibilidad de poner un texto en algún otro lugar de la figura. Con el comando

>>gtext('texto')

>>gtext('aquí esta ')

Se abrirá la figura y podremos indicar con el ratón el lugar donde ha de ir el texto, que seleccionaremos con un clic.

- Obtención de puntos desde el grafico. Una vez que se ha realizado una gráfica, podemos necesitar conocer las coordenadas de algunos puntos de la misma. Por ejemplo, el lugar aproximado en el que están los máximos y mínimos, o si queremos añadir alguna recta o una poligonal al dibujo. Para conseguir esto, se puede utilizar el comando ginput.

Escribiendo:

[x,y]=ginput(N)

Donde N es el número de puntos cuyas coordenadas queremos obtener. Después de ejecutado el comando habrá que pulsar con el botón izquierdo del ratón sobre el dibujo tantas veces como puntos hayamos especiado. Las coordenadas de esos puntos quedaran almacenadas en las variables [x; y].

>>[a,b]=ginput(10)

Al cumplir los 10 datos indicados se mostraran en la ventana de MATLAB, de a y b

a =

-2.0253

-1.8318

-1.5691

-1.3894

-1.2926

-1.1129

-1.0161

-0.8502

-0.6567

-0.4770

b =

0.0087

0.0262

0.0787

0.1429

0.1837

0.2886

0.3528

0.4810

0.6385

0.8134

GRAFICOS ESTADISTICOS

A pesar de que no se puede decir que MatLab sea el programa ideal para hacer cálculos relacionados con la Estadística, dispone de algunos comandos que nos permiten calcular algunos de los parámetros estadísticos básicos, así como comandos para generar bastantes gráficos.

Dependiendo del tipo de datos estadísticos de los que dispongamos, resulta conveniente utilizar uno u otro tipo de gráfico. Vamos a ir viendo los que se pueden hacer con MatLab, que son: diagramas de Sectores, diagramas de Pareto, diagramas de barras e histogramas.

Diagramas de sectores

Resultan útiles para representar datos de tipo cualitativo, en los que tenemos varias opciones, el diagrama de sectores permite compararlas en un círculo con sectores cuyo Angulo es directamente proporcional al porcentaje de cada opción.

Ejemplo Los resultados de los gastos de una empresa fueron los siguientes:

Elemento	gasto
Refacciones	18000
Salarios	22500
Art. Limpieza	2300
Combustibles	5600
Consumibles	2600
Varios	560

Para dibujar un diagrama de sectores de los resultados anteriores, procedemos como sigue. Introducimos los datos en un vector

>>vv=[18000 22500 2300 5600 2600 560];

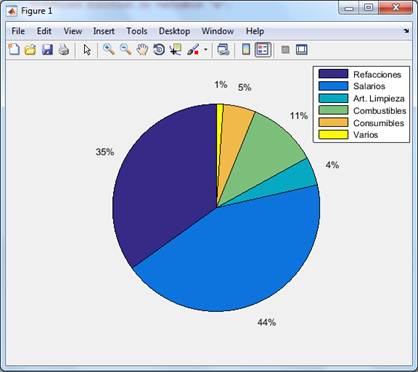
Y ahora, dibujamos el diagrama. Se puede poner una leyenda que nos indique que sector corresponde a cada gasto. Como se puede observar en el grafico (figura), MatLab calcula automáticamente los porcentajes correspondientes y los pone junto a su sector

>>pie(vv),legend(' Refacciones ', ' Salarios ',' Art. Limpieza ',' Combustibles ',' Consumibles ',' Varios ')

(Nota: si la leyenda no sale en el lugar deseado, se puede mover utilizando el botón izquierdo del ratón y colocándola en el lugar adecuado.)

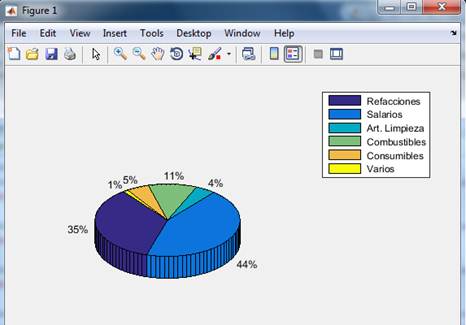
Con el comando pie3 se obtiene también un diagrama de sectores, pero en versión tridimensional.

>>pie3(vv),legend(' Refacciones ', ' Salarios ',' Art. Limpieza ',' Combustibles ',' Consumibles ',' Varios ')

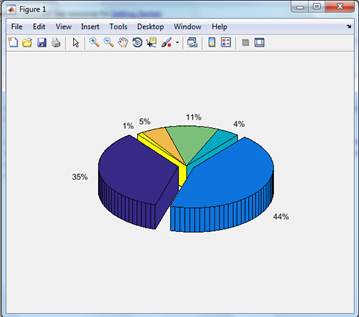
Tanto para el comando pie, como para el comando pie3 existe la posibilidad de separar uno o más sectores para destacarlos con respecto de los demás. Por ejemplo, si queremos separar los sectores correspondientes a los dos primeros datos

>>pie3(vv,[1 1 0 0 0 0])

El vector que se pone a continuación de x debe tener la misma longitud que el x, los unos y los ceros indican, respectivamente, los sectores que queremos separar y los que no.

Diagramas de barras

Existen varias posibilidades para representar diagramas de barras.

Supongamos que queremos representar los siguientes datos en un diagrama de barras:

Introducimos los datos en un vector

>>x=[10 2 3 5 18 20 15 ];

Y ahora usamos los comandos bar, barh, bar3 y bar3h para generar los gráficos. (Usando el comando subplot podemos conseguir todos en la misma figura.)

>>subplot(2,2,1),bar(x),title('Barras Verticales')

>>subplot(2,2,2),barh(x),title('Barras Horizontales')

>>subplot(2,2,3),bar3(x),title('Barras Verticales 3D')

>>subplot(2,2,4),bar3h(x),title('Barras Horizontales 3D')

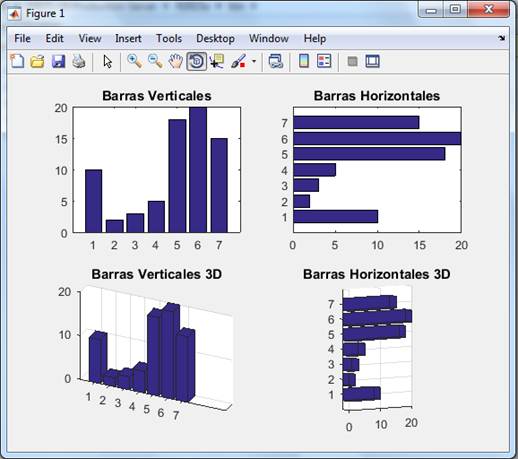
Los datos pueden estar agrupados, en este caso, las órdenes anteriores los dibujan también agrupados de manera que resulte fácil compararlos.

Veamos el siguiente ejemplo:

>>x=[1 2 3;4 3 6; 10 9 8; 4 2 7;12 10 7];

>>subplot(2,2,1),bar(x),title('Barras Verticales')

>>subplot(2,2,2),barh(x),title('Barras Horizontales')

>>subplot(2,2,3),bar3(x),title('Barras Verticales 3D')

>>subplot(2,2,4),bar3h(x),title('Barras Horizontales 3D')

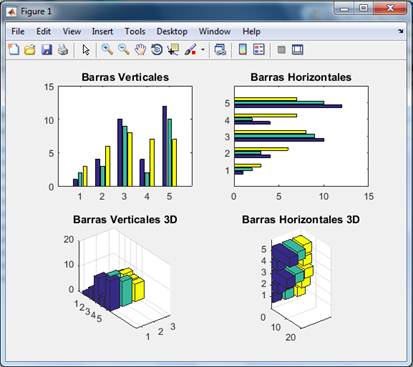
Distribuciones de frecuencias

Cuando analizamos datos la primera pregunta que debemos hacernos es si se ajustan a algún patrón. Los datos pueden ser muy numerosos y estar dispersos así que un ordenador nos puede ser de gran utilidad. Detectar el patrón depende en gran medida de la complejidad de los datos; no es lo mismo analizar cómo funciona una ruleta en un casino que hacer lo mismo con un resultado electoral.

Antes de entrar en el tema de la persistencia lo único que debemos saber a estas alturas es que para cargar estos dos archivos basta con utilizar el comando load:

(Supongamos que estamos ante una serie de datos como, por ejemplo, la cotización de las acciones)

>> op=load('open.dat');

>> cl=load('clase.dat');

Para saber el contenido de estos archivos solo basta con hacer un doble clic (botón izquierdo) en el área de las variables:

Y sobre el área de trabajo de matlab nos presentara lo que se parece a una hoja de cálculo con los datos almacenado ahí.

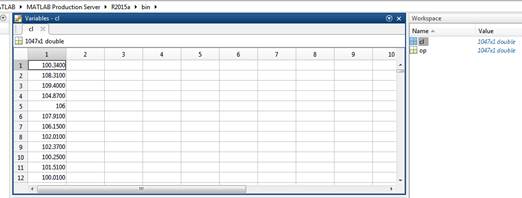
Estos pertenecen a la variable - cl (del lado derecho de la imagen se encuentran las variables y su tamaño), para cerrarla esto solo hágase un clic sobre la ventana de la hoja de trabajo en la equis:

En vez de analizar los datos de apertura y cierre (en la bolsa de valores) nos centraremos en la diferencia entre ambos valores, la cotización de la sesión, mucho más fáciles de analizar. En breve veremos el porqué.

Lo primero que podemos calcular es el histograma de nuestros datos. Podemos hacerlo de dos maneras: representando gráficamente el

histograma con hist o calculando las frecuencias con histc y utilizando el comando plot

>>dif = cl-op % se realiza la diferencia y se asigna a dif

>>bins = linspace(min(dif),max(dif),30); %linspace(x1,x2,n) genera n puntos.

%min (A) devuelve los elementos más pequeños del arreglo A

%Si A es un vector, entonces min(A) devuelve el elemento más pequeño de A

% Si A es una matriz, entonces min(A) es un vector fila que contiene el valor mínimo de cada columna.

% max(A) encuentra que el valor máximo en cada serie de datos en el momento.

>>freq = histc(dif,bins); % Recuentos de intervalos del histograma

>>plot(bins,freq);

>>xlabel('Diferencial')

>>ylabel('Frecuencia')

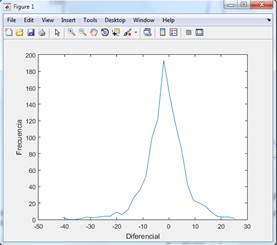
Histograma de los diferenciales del stock

(Función Densidad de Probabilidad-pdf- Una función de densidad de probabilidad caracteriza el comportamiento probable de una población en tanto especifica la posibilidad relativa de que una variable aleatoria continua, es decir permiten saber mucho acerca de una distribución de probabilidad de una sola gráfica. Puedes determinar cuál es el valor más común, cuáles son los valores más extremos y la probabilidad aproximada de cualquier valor.)

Para normalizar nuestro histograma basta con dividir las frecuencias por el valor de su integral utilizando la función trapz (normalizar.- Para evitar que los valores de un histograma sean muy dispares, se puede regularizar dicho histograma)

pdf = freq/trapz(bins,freq);

Las siguientes funciones sirven para calcular las medidas de tendencia central de una muestra.

mean(x) Calcula la media aritmética de una muestra. (N) sirve para seleccionar la dimensión a través de la cual se calcula la media en el caso que los datos tengan forma de matriz.

>>mean(cl)

ans =

404.2990
>> mean(op)

ans =

404.7861

Ejemplo en matriz

>>b = [1 2 3; 7 5 6; 4 5 6; 8 9 1]

b =

1 2 3

7 5 6

4 5 6

8 9 1

>>columnas = mean (b) % media por columnas

columnas =

5.0000 5.2500 4.0000

mean (a, dim)

- Devuelve los valores medios de la dimensión especificada de la matriz a.

- La dimensión predefinida es 1.

>>filas = mean (b, 2) % media por filas

filas =

geomean(x) Funcionamiento idéntico a mean. Calcula la media geométrica de una muestra.

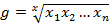
- Al igual que la función anterior, si a es un vector, calcula la media de los valores.

- Si a es una matriz, calcula la media de cada columna.

>>a = [1:10]

a =
1 2 3 4 5 6 7 8 9 10

>>mgeometrica = geomean (a)

mgeometrica = 4.5287

>> geomean(cl)

ans =

373.2626

>> geomean(op)

ans =

373.5734

harmmean(x,N) Funcionamiento idéntico a mean. Calcula la media armónica de una muestra.

Calcula la media armónica de determinados valores, en este caso representada por H, es igual al recíproco de una cantidad finita de números, o inverso, de la media aritmética de los recíprocos de dichos números, cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores y es recomendada para promediar velocidades

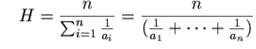
>>a = [1:10]

>>armonica = harmmean (a)

armonica = 3.4142

>> harmmean(cl)

ans =

335.2220

>> harmmean(op)
ans =

335.2506

median(x) Funcionamiento idéntico a mean. Calcula la mediana de una muestra.

>> median(cl)
ans =

422.8600

>> median(op)
ans =

424.3400

La Moda Encuentra la moda del conjunto de datos:

>> mode(cl)

ans =
180.0400

>>mode(op)
ans =

460

Medidas de dispersión.

Hay dos definiciones para la desviación típica. En algunos libros se llaman respectivamente cuasidesviación típica y desviación típica.

Para definir la desviación media y la varianza hacemos uso de la media:

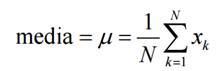
Formalmente definimos la varianza de la siguiente forma:

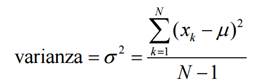
La desviación estándar (la raíz cuadrada de la varianza) se usa con más frecuencia que la varianza.

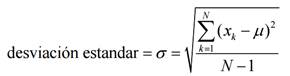
Existen definiciones alternativas para la varianza y la desviación estándar:

MATLAB puede hacer uso de estas definiciones colocando un argumento extra std (X,1) para desviación estándar y para la varianza var(X,1).

std(x,flag,dim) Calcula la desviacion estandard de una muestra

Cuando flag = 0, std (a,0) se comporta de la misma manera como std (x)

Cuando flag = 1, std (a, 1) devuelve la desviación estándar sin corregir, y el segundo momento de la muestra

Obtenemos la desviación estándar de la dimensión determinada.

Cuando dim = 0 obtenemos la desviación estándar de las columnas.

Si dim = 1 se genera la desviación estándar de las filas.

>>a = [1:10]

a =

1 2 3 4 5 6 7 8 9 10

>>Des_std = std (a) % desviación estándar corregida

Des_std =

3.0277

>>Dstd = std (a, 1)% desviación estándar sin corregir

Dstd = 2.8723% segundo momento

>>b = [1 2 3; 7 5 6; 4 5 6; 8 9 1]

>>dstd_col= std (b)% desviación estándar por columnas

dstd_col =

3.1623 2.8723 2.4495

>>dstd_fil = std (b,0,2)% desviación estándar por filas

dstd_fil =

1.0000

4.3589

>> std(cl)

ans =

142.6490

>> std(op)

ans =

143.0530

Varianza

var(x,flag,dim) Calcula la varianza de una nuestra. Es el cuadrado de la desviacion tipica.

var (a)

- Si a es un vector, retorna la varianza corregida de los valores.

- Si a es una matriz, retorna la varianza corregida de cada columna.

var (a,1)

- Si a es un vector, retorna la varianza sin corregir de los valores, mientras si a es una matriz, retorna la varianza sin corregir de cada columna.

>>a = [1:10]

a =

1 2 3 4 5 6 7 8 9 10

>>Varz = var (a) % desviación estándar corregida

Varz =

9.1667

Recordemos que: std(a) = 3.0277.

[ std(x) ]²= (3.0277) ² = 9.167 = var(x)

>>b = [1 2 3; 7 5 6; 4 5 6; 8 9 1]

b =

1 2 3

7 5 6

4 5 6

8 9 1

>>varc = var(b) % varianza por columnas

varc =

10.0000 8.2500 6.0000

>>varf = var(b,1) % varianza por filas

varf =

7.5000 6.1875 4.5000

>> var(cl)

ans =

2.0349e+04

>> var(op)

ans =

2.0464e+04

Range () Devuelve el rango de una determinada serie de datos, es decir calcula la diferencia entre el dato máximo y el dato mínimo.

range (a)

- Si a es un vector, calcula el rango del mismo.

- Si a es una matriz, calcula el rango de cada columna.

>>a = [1:10]

>>rango = range (a)

rango=

>>b=[123;756;456;891]

1 2 3

7 5 6

4 5 6

8 9 1

ran = range (b)

ans=

641.9400

Distribución de frecuencia acumulada

>>cdfplot(cl)
cdfplot(op)

El máximo y el mínimo

max(x) si x es vector encuentra el valor más grande, si x es matriz crea un vector que contiene el elemento máximo de cada columna.

>>max(cl),min(cl)

>>max(op),min(op)

[a , b]=max (x) encuentra el valor más grande (a) de x y su posición (b).

>> [a , b]=max (cl)

a =

741.7900

b =

811

>> [a , b]=max (op)

a =

741.1300

b =

812

max(x,y) si x y y tienen las mismas dimensiones devuelve una matriz cada entrada es el máximo de las entradas correspondientes de x y y.

De manera análoga ocurre con la función min.

>> [a , b]=min (cl)

a =

100.0100

b =

>> [a , b]=min (op)

a =

99.1900

b =

Sumas y productos

Con frecuencia es útil sumar todos los elementos en una matriz o multiplicar todos los elementos juntos. MATLAB proporciona algunas funciones para calcular tanto sumas como productos, además de sum y prod

cumsum(x) si x es vector devuelve un vector del mismo tamaño que x con las sumas acumuladas, si x es matriz entonces calcula la suma acumulada de los elementos en cada columna.

>> cumsum(cl)

ans =

1.0e+05 *

0.0010

0.0021

0.0032

……

>> cumsum(op)

ans =

1.0e+05 *

0.0010

0.0020

0.0031

…….

cumprod(x) análoga a cumsum pero para el producto.

>> cumprod(cl)

ans =

1.0e+306 *

0.0000

…..

>> cumprod(op)

ans =

1.0e+306 *

0.0000

…..

Ordenamientos

sort(x) Ordena los elementos de un vector x en orden ascendente u ordena los elementos en cada columna de una matriz x en orden ascendente.

>> as=sort(cl)

as =

100.0100

100.2500

100.3400

101.5100

101.5800

102.0100

102.3000

….

718.4200

725.6500

732.9400

741.7900

>> as1=sort(op)

as1 =

99.1900

100.0000

100.7400

100.9500

…………

719.9400

734.6000

737.5600

741.1300

sort (x, 'descend') Ordena en forma descendente y funciona de manera análoga a sort.

>> as=sort (cl, 'descend')

as =

741.7900

732.9400

725.6500

718.4200

…….

100.3400

100.2500

100.0100

>> as=sort (op, 'descend')

as =

741.1300

737.5600

734.6000

719.9400

…….

100.9500

100.7400

100.0000

99.1900

sortrows(x) Ordena las filas en una matriz sobre la base de los valores en la primera columna.

>> sortrows(cl)

ans =

100.0100

100.2500

100.3400

101.5100

sortrows(x,n) Ordena las filas en una matriz sobre la base de los valores en la n-ésima columna.

Determinación del tamaño de matriz

Para determinar el tamaño de una matriz usamos : size y length.

>> size(cl)

ans =

1047 1 % Número de elementos y columnas.

>> length (cl) % tamaño de una matriz

ans =

1047

>> size(op)

ans =

1047 1% Número de elementos y columnas

>> length (op)

ans =

1047