LA MEDIANA
Mediana (Me): Valor que divide una serie de datos en dos partes iguales.
La cantidad de datos que queda por debajo y por arriba de la mediana son iguales.
La definición de geométrica se refiere al punto que divide en dos partes a un segmento. Por ejemplo, la mediana del segmento AB es el punto C.

Existen entonces dos segmentos iguales:
![]()
Ejemplo: mediana para datos no agrupados (cantidad de datos impar)
Encontrar la mediana para los siguientes datos:
4 1 2 3 4 2 2 1 5 5 3
SOLUCIÓN
PASO 1: Ordenar los datos.
1 1 2 2 2 3 3 4 4 5 5
PASO 2: Localizar el valor que divide en dos parte iguales el número de datos.

La mediana es 3, dejando 5 datos a cada lado.
Me = 3
Ejemplo: mediana para datos no agrupados (cantidad de datos par)
Modifiquemos el ejemplo anterior, eliminando el último dato. Encontrar la mediana:
4 1 2 3 4 2 2 1 5 5
SOLUCIÓN
PASO 1: Ordenar los datos.
1 1 2 2 2 3 4 4 5 5
PASO 2: Localizar el valor que divide en dos parte iguales el número de datos.

El punto medio se encuentra entre dos valores: 2 y 3, por tanto, el valor de la mediana será 2,5.
Me = 2,5
Ejemplo: mediana para datos agrupados en tablas tipo A
Calcular la mediana a partir de la siguiente tabla de frecuencia:
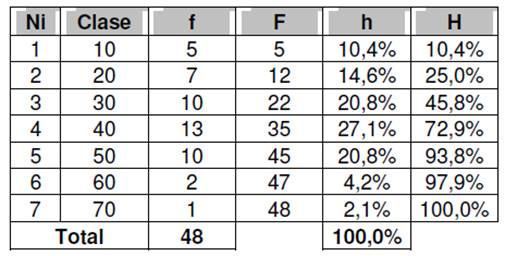
SOLUCIÓN
PASO 1: Localizar entre que clases se encuentra la mediana. Observe que la mediana se encuentra entre las clases 3 y 4, donde podremos encontrar una Frecuencia relativa acumulada del 50%.
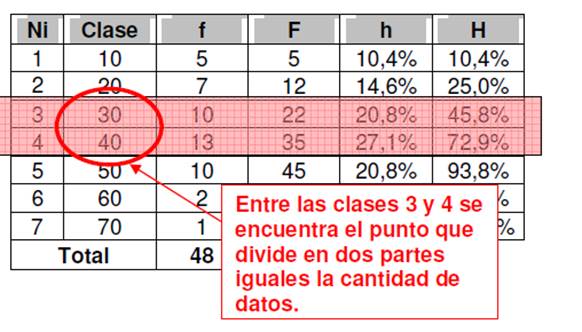
PASO 2: Interpolar los datos para encontrar la mediana.
En el paso anterior habíamos dicho que el punto que divide el 2 parte iguales se encuentra entre 30 y 40.
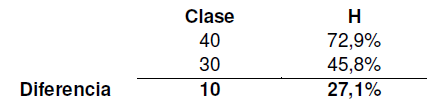
La diferencia entre las frecuencias relativas nos indica que existe entre las clases 27,1% de los datos. Para llegar al 50% de los datos, debemos incrementar en 4,2% datos partiendo desde la clase 30.
50,0% = 45,8%+ 4,2%
Con una regla de tres sencilla hallaremos el incremento en unidades dada en la clase para ese 4,2%.
10 -------------- 27,1%
Incremento ------------4,2%
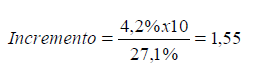
Para llegar al 50% de los datos, a la clase 30 debemos incrementarle 1,55.
Me = 31,55
Ejemplo: mediana para datos agrupados en tablas tipo B
Determinar la mediana de la siguiente tabla de frecuencia:
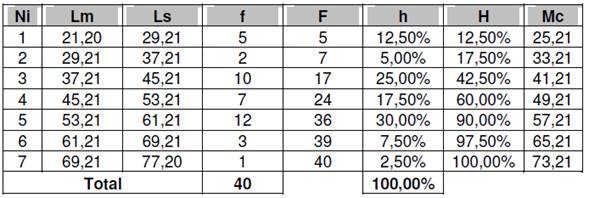
SOLUCIÓN
PASO 1: Localizar entre que intervalos de clase se encuentra la mediana.
Podemos observar que el punto que divide el 50% de los datos esta entre el intervalo de clase 3 y 5, para ser más preciso, entre los valores 45,21 y 53,21 (hasta 45,21 hay agrupados el 42,50% de los datos, y hasta 53,21 se resume el 60,00% de los datos).
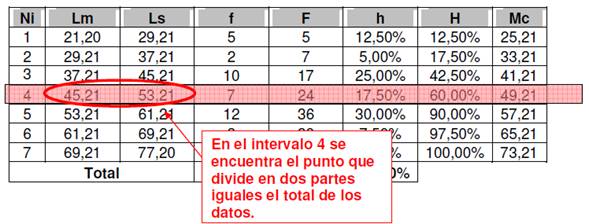
PASO 2: Interpolar los datos para encontrar la mediana. En resumen tenemos
que:

Entre los dos límites superiores abarcan un total de 17,50% de los datos. Se debe aumentar en 7,50% los datos desde límite superior del tercer intervalo de clase.

Para llegar al 50% de los datos, 45,21 se aumenta en 3,43 unidades.
Me = 45,21+ 3,43
Me = 48,64
Calculo de la mediana en Excel
Excel posee la función MEDIANA para el cálculo de la mediana en datos no agrupados.
MEDIANA: Calcula la mediana para una serie de datos.
Formato: MEDIANA(número1;número2;…)
Categoría: Estadísticas
Copie los datos dados a partir de la celda B2:

Active la función MEDIANA en la celda B4 y en el campo número1 seleccione los datos del ejercicio.
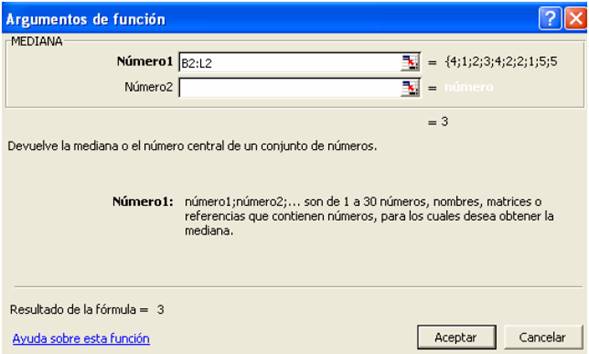
La mediana en este caso es 3:

Ventajas
Es estable a los valores extremos.
Es recomendable para distribuciones muy asimétricas.
Desventajas
No presenta todo el rigor matemático.
Se emplea solo en variables cuantitativas.