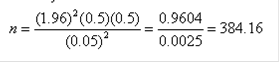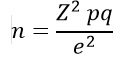Presentación de la unidad
La palabra estadística a menudo te remite a gráficas y tablas; cifras relativas a nacimientos, muertes, impuestos, demografía, ingresos, deudas, créditos, etc. No obstante, para aprovechar las herramientas de análisis estadstico, es necesario comprender qué representa cada concepto y la metodología mediante la cual se obtiene un dato estadístico.
En esta unidad se hablará sobre la importancia de la estadística, conocerás sus conceptos básicos, así como la metodología del muestreo para que al final, obtengas una muestra aleatoria simple.
Indice de temas que componen esta unidad.
Identificarás los conceptos básicos relacionados con la Estadística.
Reconocerás la utilidad e importancia de la Estadística.
Conceptos de estadística
Muestreo aleatorio
Muestreo
simple
aleatorio
Problemas
Competencia específica
Aplica la metodología estadística para obtener una muestra aleatoria simple, identificando los elementos que intervienen en un problema estadístico.
1.1. Introducción a la estadística
La estadística es la
ciencia cuyo objetivo es reunir información cuantitativa
relacionada a individuos, grupos, series de hechos, entre otros.
Gracias al análisis de estos datos se pueden deducir algunos
significados precisos o algunas previsiones para el futuro. La
estadística, en general, es la ciencia que trata la
recopilación, la organización, la presentación, el análisis y la
interpretación de datos numéricos con el fin de realizar una
toma de decisiones más efectiva.
La estadística
La palabra estadística también se utiliza para referirse a la información estadística(descripción de parámetros); es decir, la series de datos, tablas y gráficas que presentan resultados. Por ejemplo, cuando leemos las estadísticas de los equipos o escuchamos la estadística muestra que el índice de reprobación en las escuelas es tal, se hace referencia a los datos y no al procedimiento o metodología de análisis.
Utilidad e importancia de la estadística.
La estadística resulta muy útil no sólo para recopilar y describir datos, sino también para interpretar la información obtenida, que puede ser aprovechada para demostrar la evolución de un fenómeno a través de cierto tiempo.
En México, el Instituto Nacional de Estadística y Geografía (INEGI) se encarga de recabar información estadística y geográfica de todo el país, en diferentes áreas y contextos.
Los métodos estadísticos se utilizan en investigaciones de todas las áreas del conocimiento en el ámbito académico, profesional y laboral. La finalidad es resolver un problema, entendiendo éste como la diferencia entre lo real y lo deseado, donde la estadística muestra la realidad para que el investigador la analice y tome una decisión.
1.2.Conceptos de estadística
La estadística tiene aplicación en prácticamente todas las áreas del conocimiento, inclusive en la vida cotidiana, mucho más a menudo de lo que crees.
La siguiente actividad te permitirá apreciar una aplicación simple de la estadística e identificar algunos conceptos relacionados con ella:
Carlos presenta síntomas de una infección, su doctor le indica acudir a un laboratorio para tomarse una muestra de sangre a partir de la cual se realizarán estudios clínicos y determinar si los signos corresponden a dicha enfermedad.
Los técnicos del laboratorio extraen algunos mililitros de sangre para realizar un conteo de Globulos Blancos, que segun su conteo (dentro de los globulos blancos, hay una variedad de ellos que sirven para contrarestar a las bacterias que pudieran entrar al cuerpo, como por una herida). El médico interpreta el resultado del análisis comparándolo contra los parámetros normales para diagnosticar adecuadamente si es una infección por bacterias o virus a Carlos, antes de seguir tenemos que comprender los siguientes conceptos
Los conceptos más utilizados en estadística son los que a continuación se presentan.
|
Población: Conjunto de todos los elementos que permiten resolver un problema, que presentan una característica común determinada, observable y medible. Por ejemplo, si el elemento es una persona, se pueden estudiar las características edad, peso, nacionalidad, sexo, etc. Los elementos que integran una población pueden corresponder a personas, objetos o grupos (por ejemplo, familias, las manzanas de una cosecha, empleados de una empresa, etc.).
|
|
Individuo: Un
individuo o unidad estadística es cada uno de los
elementos que componen la población. Nota que un
individuo en estadística puede ser distinto a un
individuo como persona. Por ejemplo, en los censos
económicos se obtienen datos de los negocios. En
este caso cada negocio, que está formado por varias
personas, es un individuo de la población.
|
|
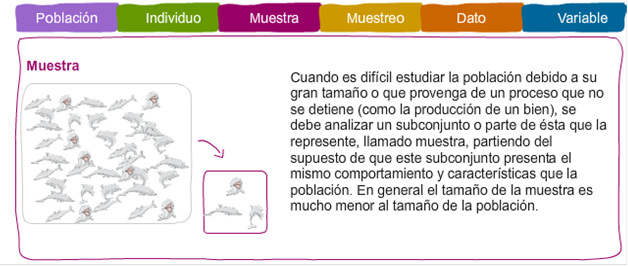
Muestra:
Cuando es difícil estudiar la población debido a su
gran tamaño o que provenga de un proceso que no se
detiene (como la producción de un bien), se debe
analizar un subconjunto o parte de ésta que la
represente, llamado muestra, partiendo del supuesto
de que este subconjunto presenta el mismo
comportamiento y características que la población.
En general el tamaño de la muestra es mucho menor al
tamaño de la población.
|
|
Muestreo: Es el
proceso de recabar los datos que se desean analizar,
obtenidos de una proporción reducida y
representativa de la población.
|
|
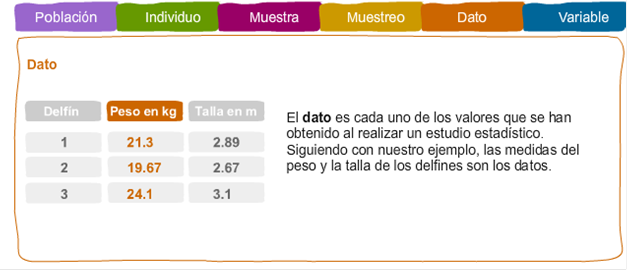
Dato: El
dato es cada uno de los valores que se han obtenido
al realizar un estudio estadístico. Por ejemplo: Si
lanzamos una moneda al aire 5 veces obtenemos 5
datos: cara, cara, cruz, cara, cruz.
|
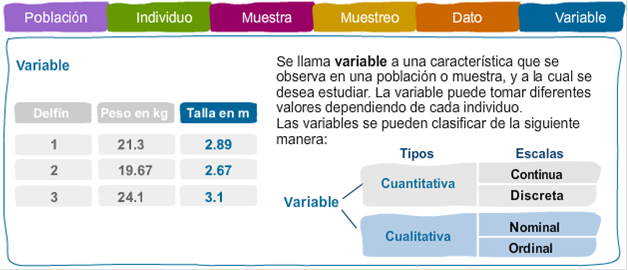
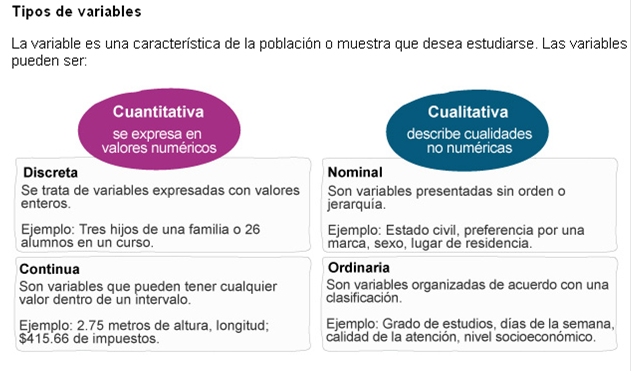
Variable: Se llama variable a una característica que se observa en una población o muestra, y a la cual se desea estudiar. La variable puede tomar diferentes valores dependiendo de cada individuo. Las variables se pueden clasificar en dos tipos:
1. Variable cuantitativa. Puede ser escala continua o discreta.
2. Variable cualitativa. Puede ser escala nominal u ordinal.
Cómo utilizamos los conceptos?
En el ejemplo que habiasmos comenzado la estadística y la salud identificaste algunos conceptos básicos de estadística. Ahora, revisemos los conceptos que estaban en el texto.
La población de estudio es la sangre del individuo, de la cual se toma una muestra que representa una pequeña parte de esta población. Esta muestra contiene información sobre las características que se desean observar.
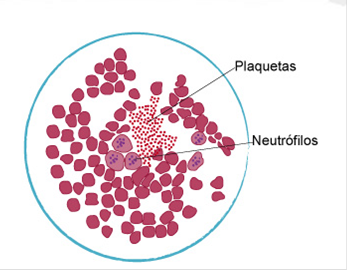
Los (las) expertos(as) de laboratorio preparan la sangre para observar en un microscopio, los elementos (variables) que contiene, por ejemplo pueden observar la cantidad de globulos blancos (los globulos blancos están presentes en varios tipos de células espécialilizadas, como son Basofilos, Neutrófilos, Segmentados, Linfocitos, Eosinofilos, Nonocitos, cada uno tiene una fución especifica y única, y su ausencia o aumento representa una alteración que se presenta por una enfermedad) son los individuos y los contiene la sangre de estos elementos son los datos que contiene la muestra por unidad de volumen.
Se realiza un conteo, en este caso, del número de plaquetas y del número de neutrófilos, esta información se representa por medio de un estadístico, característica numérica que refleja la información contenida en la muestra, en la que se observa el total de globulos blancos (con sus variedades) y plaquetas.
Aunque, en realidad, lo que nos interesa conocer o estimar es el total de plaquetas en el total de la sangre (población) del individuo.
Cuántos conceptos identificaste en la lectura?
|
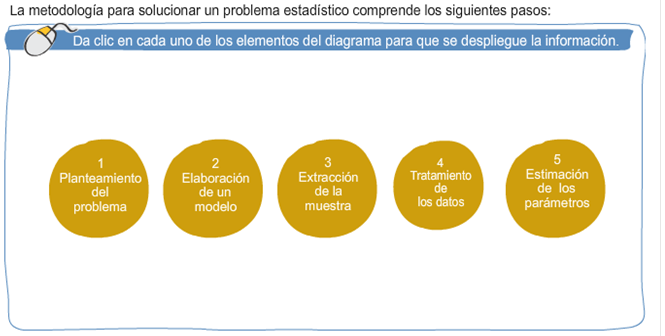
1.
Planteamiento del problema. En el
planteamiento se define si se requiere de una
muestra o es posible estudiar la población, las
características a estudiar (las variables), si es
necesario establecer una hipótesis, entre
otros. En este punto también se analizan los medios
de los que se dispone y el procedimiento a seguir. |
|
2.
Elaboración de un modelo. Se
establece un modelo teórico de comportamiento de las
variables de estudio. En ocasiones no es posible
diseñar el modelo hasta realizar un estudio previo.
|
|
3.
Extracción de la muestra. Se usa
alguna técnica de muestreo o un diseño experimental
para obtener información de una pequeña parte de la
población. |
|
4.
Tratamiento de los datos. En
esta fase se eliminan posibles errores, se depura la
muestra, se tabulan los datos y se calculan los
valores que serán necesarios en pasos posteriores,
como la media y la varianza de la muestra. Los
métodos de esta etapa corresponden a los métodos de
la estadística descriptiva. Algunas de las etapas de
esta fase son: recopilación, clasificación y
presentación de la información. |
|
5.
Estimación de los parámetros. La
estadástica inferencial nos proporciona herramientas
para la predicción o estimación de los parámetros de
la poblacion que nos ayudarán a resolver el
problema. Un ejemplo de estas herramientas son las
pruebas de hipótesis que se obtienen del análisis de
los datos y los intervalos de confianza. |
1.3 Muestreo aleatorio.
Introducción
Los estudios estadísticos normalmente se hacen con una parte de la población, ya que realizarlos sobre la totalidad resultaría demasiado complicado. Para que la información obtenida tenga validez y confiabilidad es necesario que la muestra cumpla con ciertas condiciones específicas.
Estas condiciones están relacionadas con el método para determinar el tamaño y características de la muestra y los individuos que la componen.
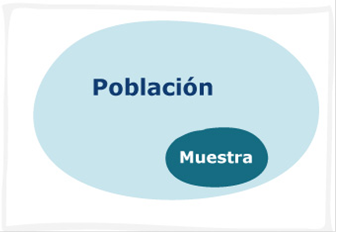
Los métodos de muestreo se pueden clasificar en:
Dentro de los
métodos de muestreo probabilístico se encuentra, además del
muestreo aleatorio simple (que revisarás con detalle más
adelante), los siguientes tipos:
Muestreo Sistemático: Es aquel en el que los elementos de la población que conformarón la muestra se seleccionan en intervalos regulares, es decir, se numeran los elementos de la población, se escoge uno al azar i y todos los elementos i + k, se seleccionan para la muestra. Ejemplo: de una población de 1000 individuos se quiere seleccionar 100, la selección al azar del número i, da como resultado el individuo 13 de la población, entonces la muestra se obtiene seleccionando la unidad 13, la 26, la 39, hasta que se obtienen 100 observaciones.
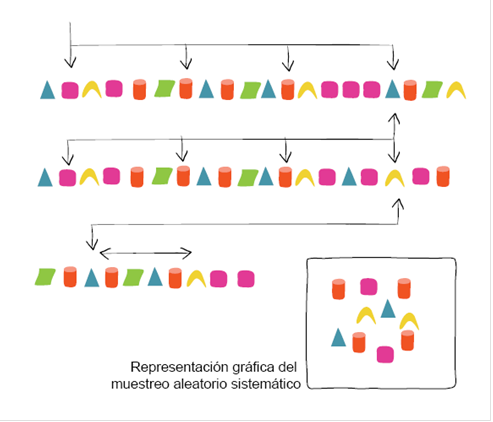Muestreo estratificado
En este tipo de muestreo, la población es clasificada en categorías diferentes entre sí, llamadas estratos, que poseen gran homogeneidad respecto a alguna característica (por ejemplo profesión, sexo, estado civil, etc.). Lo que se pretende con este tipo de muestreo es asegurarse de que todos los estratos de interés estarán representados adecuadamente en la muestra.
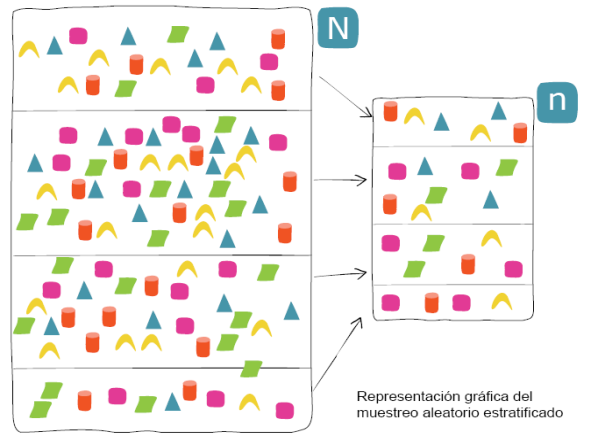
Cada estrato funciona independientemente, pudiendo aplicarse dentro de ellos, nuevamente, el muestreo aleatorio simple o el estratificado para elegir los elementos concretos que formarán parte de la muestra.
Muestreo aleatorio por conglomerados: En este tipo de muestreo cada unidad o individuo de la muestra esté formado por un grupo de elementos, al que se le llama conglomerado, este grupo contiene representantes de toda la población (de acuerdo a la característica que se mida).
El muestreo por conglomerados consiste en seleccionar aleatoriamente el número de conglomerados necesario para alcanzar el tamaño muestral, en el cual se investigan a todos los elementos que componen los conglomerados elegidos.
Muestreo mixto: Este consiste en la combinación de dos o más tipos de muestreo vistos anteriormente. Por ejemplo, si se desea estudiar una producción de medicinas puede hacerse primero un muestreo aleatorio por conglomerados y escogerse ciertos lotes. Sobre estos lotes se hace luego un sistemático y se selecciona uno de cada 29 frascos de medicina del lote.
1.3.1. Conceptos
básicos de muestreo
Muestreo aleatorio
simple
El muestreo
aleatorio simple es el procedimiento por medio del cual se
obtiene una muestra aleatoria simple.
Una muestra
aleatoria simple es la que resulta de aplicar un método por el
cual todos los elementos de la población tienen la misma
probabilidad de ser elegidos.
A continuación,
conocerás cuáles son los pasos para obtener una muestra
aleatoria simple.
|
Paso 1. Definir la
población de estudio y el parametro a estudiar. |
|
Paso 2. Enumerar a
todas las unidades de análisis que integran la
población, asignándoles un número de identidad o
identificación. |
|
Paso 3. Determinar
el tamaño de la población, determinar el porcentaje de
error y el porcentaje de confianza y obtener una
muestra preliminar. |
|
Paso 4. Determinar
el tamaño óptimo de la muestra para el estudio. |
|
Paso 5.
Seleccionar los sujetos dela muestra usando números
aleatorios. |
|
Pasos
para obtener una muestra aleatoria simple |
||
|
Has visto
una descripción general del procedimiento que debes
seguir para obtener una muestra aleatoria simple,
ahora revisarás cada paso especéfico. |
||
|
||
|
Recuerda
que la población
es el grupo formado por el conjunto
total de individuos, objetos o
medidas que poseen algunas características comunes,
observables en un lugar y en un momento determinado.
Por lo tanto, el paso 1 es determinar qué se
estudiará. |
Ejemplo
Un investigador realiza un estudio sobre las relaciones de
género en el noviazgo, su objeto de estudio son las
manifestaciones de violencia física y psicológica entre los
(las) estudiantes del último año de la carrera de química. Su
población es el total de estudiantes del último año de
ingeniería química que tengan novio o novia; el total de
individuos con esta caracteréstica es de 386. Por lo que, la
población es de 386 individuos y las variables son: violencia
física y violencia psicológica
|
||
|
Una vez que
has definido la población y las variables a estudiar,
es necesario asignar un número de identificación a
cada individuo de la población. Siguiendo
con el ejemplo de la relaciones de género en el
noviazgo de los (las) estudiantes de química, lo que
sigue es numerar a los 386 estudiantes un número del 1
al 386. |
|
||
|
Para
calcular el tamaño de una muestra hay que tomar en
cuenta tres factores: 1. El
porcentaje de confianza con el que se quiere
generalizar los datos, desde la muestra hacia la
población total. 2. El
porcentaje de error que se pretende aceptar al momento
de hacer la generalización. 3. El nivel
de variabilidad que se calcula para comprobar la
hipótesis. A
continuación definiremos estos conceptos. |
Ahora
veamos una definición de los conceptos implicados en el paso
3.
|
Definir
el tamaño de la población. Significa
determinar el número de individuos que la constituyen;
la variable N representa el tamaño de la población.
N=X |
|
Porcentaje
de confianza. Es el
grado o nivel de seguridad que existe para generalizar
los resultados obtenidos. Esto quiere decir que un
porcentaje del 100% equivale a decir que no existe
ninguna duda para generalizar tales resultados, pero
también implica estudiar a la totalidad de los casos
de la población. Para evitar un costo muy alto se
busca un porcentaje de confianza menor, comúnmente es
un 95%. El nivel de confianza es la probabilidad que
establecemos (sin hacer ningún cálculo) para poder
acertar al valor verdadero de la población
. Este dato se obtiene a partir de la
distribución normal estándar. |
|
Porcentaje
de error. Este error
es una distancia alrededor del valor que deseamos
estimar y nos da un margen de aproximación. Al igual
que en el caso de la confianza, si se quiere eliminar
el riesgo del error y considerarlo como 0%, entonces
la muestra es del mismo tamaño que la población, por
lo que conviene correr un cierto riesgo de
equivocarse. Comúnmente se aceptan entre el 4% y el 6%
como error, tomando en cuenta de que no son
complementarios la confianza y el error. |
|
Variabilidad. Es la
probabilidad (o porcentaje) con el que se aceptá y se
rechazá la hipótesis que se quiere comprobar. El
porcentaje con que se aceptá tal hipótesis se denomina
variabilidad
positiva y se indica con p
(también llamada probabilidad de éxito
), y el porcentaje con el que se rechazá la
hipótesis es la variabilidad
negativa, identificada por q
(también llamada probabilidad de fracaso y se obtiene
1-p). Variabilidad
positiva=p= a la probabilidad de que suceda el evento La
variabilidad positiva (p)
al sumarla con la negativa (q)
siempre nos debe dar la unidad p+q=1.Cuando
no se
tienen antecedentes sobre la investigación, entonces
los valores de variabilidad son p=q=0.5 |
|
||
|
Una vez que
la población, el porcentaje de confianza, el
porcentaje de error y el nivel de variabilidad han
sido determinados, se debe determinar el tamaño de la
muestra. Puedes
calcularlo mediante alguna de las dos fórmulas que
examinarás: una para los casos en que se conoce el
tamaño de la población y la otra para cuando este dato
se desconoce. |
Fórmula
para cuando no se conoce el tamaño de la población
|
|
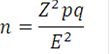
n es el
tamaño de la muestra |
Ejemplo:
Solución:
Para el nivel de confianza sea igual al 95%, tienes que P(Z)=0.95 si Z=1.96. (ver tabla donde se obtiene este dato, en esta tabla se puede apreciar)
Es recomendable revisar el siguiente documento para comprender mejor el nivel de confianza
Debido a que la variabilidad y el error se pueden expresar por medio de porcentajes, en el caso necesario, hay que convertir esos valores a proporciones.
Sustituyendo:
|
|
Es decir, se
ocupará una muestra de aproximadamente 384 unidades.
Fórmula
para cuando se conoce el tamaño de la población
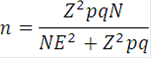
n
es el tamaño de la muestra
Z
es el nivel de confianza
p es
la
variabilidad positiva
q es
la
variabilidad negativa
N es
el
tamaño de la población
E
es la precisión o error
Ejemplo:
Solución:
Para el nivel de confianza sea igual al 95%, tienes que p(Z)=0.95 si Z=1.96. Sustituyendo:
En otras palabras, se ocupará una muestra de aproximadamente
378 cajas
|
|
||
|
|
|
||
|
|||
|
El último
paso para obtener la muestra es saber qué individuos
específicos de la población se tomarán. Para hacer
esto debes: 1. Numerar
a los individuos de la población del 1 a N (donde N es
el tamaño de la población). 2. Generar
números aleatorios para seleccionar los individuos de
la muestra. 3. Tomar
los individuos correspondientes a los numeros
elegidos. |
|||
Los números
aleatorios se pueden generar por diversos métodos, por ejemplo
mediante programas computaciones (por ejemplo en Excel con la
función =aleatorio() ), funciones
en calculadora, sacando números de una urna o lanzando una
moneda al aire, o bien utilizando tablas de números
aleatorios. Para obtener los números aleatorios, utilizarás la
tabla, para ello lee
el documento Uso_de_la_tabla_de_números_aleatorios..pdf
1. Determinar el nivel de confianza con que se desea trabajar. (Z ), donde
z = 1.96
para un 95% de confianza ó z = 1.65 para el 90% de confianza
|
TABLA DE APOYO AL CALCULO
DEL TAMAÑO DE UNA MUESTRA POR
NIVELES DE CONFIANZA |
|||||||||
|
Certeza |
95% |
94% |
93% |
92% |
91% |
90% |
80% |
62.27% |
50% |
|
Z |
1.96 |
1.88 |
1.81 |
1.75 |
1.69 |
1.65 |
1.28 |
1 |
0.6745 |
|
Z 2 |
3.84 |
3.53 |
3.28 |
3.06 |
2.86 |
2.72 |
1.64 |
1.00 |
0.45 |
|
e |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
0.10 |
0.20 |
0.37 |
0.50 |
|
e2 |
0.0025 |
0.0036 |
0.0049 |
0.0064 |
0.0081 |
0.01 |
0.04 |
0.1369 |
0.25 |
Esta distribución normal, nos permite representar en la estadística muchos fenómenos físicos, biológicos, psicolólogicos o sociológicos.
Ahora bien, se hace necesario el definir los térmnos Media, Moda y Mediana.
MEDIA: Es el conjunto de n observaciones sumadas y divididas entre n.
MODA: Se define como el valor que mas ocurre en un conjunto de observaciones.
MEDIANA: Es el centro de un conjunto de observaciones ordenadas en forma creciente.
2.-
Considerar que los valores p y q, que se realice (p) y
la de que no se realice (q); siempre tomando en
consideración que la suma de ambos valores p + q será
invariablemente siempre igual a 1, cuando no contemos con
suficiente información, le asignaremos p = .50 q = .50
3. Determinar el grado de error máximo aceptable en los resultados de la investigación. Éste puede ser hasta del 10%; ya que variaciones superiores al 10% reducen la validez de la información.
Se aplica la fórmula del tamaño de la muestra de acuerdo con el tipo de población
|
Población
infinita |
Población
Finita |
|
|
|
|
Cuando no
se sabe el número exacto de unidades del que está
compuesta la población. |
Cuando se
conoce cuántos elementos tiene la población |
|
En donde: Z = nivel de
confianza. p = Probabilidad a favor. q =
Probabilidad en contra. q=p-1 Probabilidad en contra. n = tamaño de la muestrae = error de estimación. |
En donde: N = Universo Z = nivel de
confianza. p = Probabilidad a favor. q =
Probabilidad en contra. q=p-1 Probabilidad en contra. n = tamaño de la muestrae = error de estimación. |
Ejemplo
aplicado
Supóngase
que se desea determinar la calidad y el nivel de servicio que
ofrece nuestra Unidad de información de Archivo; por lo que
resulta necesario entrevistar a los distintos usuarios que
acuden a nuestro archivo para así conocer su opinión. Cómo
calcularíamos el tamaño de la muestra?
1.Establecer
el nivel de confianza (95% y un error del 5%) o el (90% - y un
error del 10%).
2.Se
obtiene el marco muestral, en este caso la referencia con que
contamos será el registro de visitantes a
nuestra Unidad de Información del año pasado y que arroja la
cifra de 43,700.
Valores
a estimar
n
= ?
e
= 5% =0.05 o 10% = 0.1
Z
= 1.96 (tabla de distribución normal para el 95% de
confiabilidad y 5% error) o
Z
= 1.65 para el 90% de confiabilidad y 10% error.
N= 43,700
(universo)
p
= 0.50
q
= 0.50
3
Enseguida
especificaremos las operaciones para evaluar a n (tamaño de la
muestra) , Para ésta estimación
supondremos que contamos con un 95% de confiabilidad y por
tanto un porcentaje de error del 5% (0.05)
4. Ahora
bien, si nuestro criterio fuera otro como por ejemplo el
considerar un margen del 90% de confiabilidad con su
correspondiente porcentaje de error, en este caso sería del
10% 0.10)
1. Un lingúista
quiere estudiar cuáles son las vocales más usadas dentro de
las palabras en un texto de alrededor de tres mil palabras.
Contar palabra por palabra sería demasiado trabajo. Por lo que
se analizará un subconjunto representativo.
Resuelve las
siguientes cuestiones:
a) Cuál es la
población de estudio?
b) Cuáles son los
individuos de esa población?
c) De cuántos
individuos consta la población? Numéralos comenzando por el
00.
d) Cuál es la
variable o cuáles son las variables a estudiar?
e) Cuál debe ser el
número de elementos necesarios para tomar una muestra
aleatoria simple tal que los resultados del estudio tengan un
porcentaje de error de 5% y un porcentaje de confianza de 95%?
Para calcularlo, considera que Z= 1.96 y que la variabilidad
positiva es igual a la negativa.
f)
Con el resultado anterior:
Obtén la muestra a
partir de una tabla de números aleatorios.
Elabora una lista
de los datos obtenidos de la muestra de acuerdo con las
variables que señalaste en el inciso d.
2.
Determina
los elementos necesarios para saber cuál es el color que se
presenta con mayor frecuencia en los carros de tu colonia.
a)
Cuál es la población de tu estudio?
b)
Cuáles son los individuos de esa población?
c)
Puedes determinar de cuántos individuos consta la población?
Si es posible, numéralos comenzando por 00. Si no es posible,
explica por qué.
d)
Cuál es la variable o cuáles son las variables a estudiar?
e)
Obtén el número de elementos necesarios para tomar una muestra
aleatoria simple tal que los resultados del estudio tengan un
porcentaje de error de 5% y un porcentaje de confianza de 95%?
Para calcularlo, considera que Z= 1.96 y que la variabilidad
positiva es igual a la negativa.
En ocasiones
recurrimos a ella para solucionar problemas y tomar
decisiones. También es una metodología muy útil para presentar
información y analizar diferentes situaciones de la vida
cotidiana.
Los conceptos
básicos que revisaste son:
Estadística
descriptiva
Estadística
inferencial
Población
Individuo
Dato
Parámetro
Variable
Muestreo
Actividad para desarrollar:
En esta seccion deberas de volverte un observador, tu tarea
deberas de realizar una tabla donde anotes los siguintes
datos:
en cuanto vayas a algún lugar anota el color de los autos que veas en el trayecto , colores como rojo, azul, verde, etc. no importa el tono solo el color principal, y realizaremos un estudio estadistico de esto te llevaras una sorpresa.
Puedes realizar un estudio estadistico de cualquier cosa,
donde intervengan muchas presonas u objetos, sera muy
interesante ver los resultados de tus estudios.
Dentro
de
los tipos de muestreo, te centraste en el muestreo
probabilístico y pusiste especial énfasis en el muestreo
aleatorio simple, en el que todos los individuos de la
población tienen las mismas posibilidades de ser elegidos.
El procedimiento
para obtener una muestra aleatoria simple consiste en
determinar la muestra y seleccionar a los individuos de la
población que formarán parte de ella. Esta selección se lleva
a cabo a través de números aleatorios, que se pueden generar
de varias formas: aplicaciones informáticas para estadística,
calculadoras, tablas de números aleatorios, etc.