
Presentación de la unidad
Unidad 2. Representación numérica y gráfica de datos
En la unidad anterior, conociste
las dos grandes divisiones de la estadística: la que se dedica a
la recolección, presentación y categorización de datos, llamada
estadística descriptiva y la que se dedica a realizar hipótesis
con base en dichos datos, la inferencial.
También aprendiste a determinar
el espacio de estudio (es decir, la población) y las variables
que se van a estudiar de acuerdo al problema planteado.
En esta unidad estudiarás la estadística descriptiva y aprenderás cómo organizar y presentar los datos obtenidos mediante el muestreo en poblaciones.

Otra de las técnicas más recurridas en estadística para recolectar información son los experimentos, revisa en qué consisten.
Un experimento es una prueba que se realiza para determinar las características o comportamientos de una cosa. Por ejemplo, experimentar mediante el sentido del gusto, qué alimentos te parecen más salados.
También, experimento se define como el proceso que se realiza para verificar una serie de hipótesis relacionadas con un determinado fenómeno, en el cual se determinan las características o comportamientos del fenómeno que se analiza.
Por ejemplo, un experimento para determinar la velocidad de la luz en el vacío.
La diferencia entre la primera y
la segunda definición, es que en la segunda se parte de una
hipótesis mientras que en la primera no necesariamente.
En el primer ejemplo, experimentas los sabores de los alimentos sin antes predecir cuál será más salado. En el segundo ejemplo, la hipótesis, a partir de estudios anteriores, es que la velocidad de la luz en el vacío es de 300,000 km/seg.
Por lo tanto, el experimento verifica si esta hipótesis es cierta o no y en él cabe un margen de error experimental.
Los datos que se recopilan, usando alguna técnica de las que acabamos de describir u otra, son organizados de acuerdo a los parámetros de la estadística descriptiva que se estudiarás en esta unidad.
Propósitos de la unidad
En esta unidad:
1.- Identificarás algunos conceptos que se utilizan en estadística descriptiva.
2.-Definicion
de
datos agrupados y no agrupados
3.- Frecuencias
4.- Intervalos
5.- Costrucción de intervalos de clase
6.- Tablas de datos
7.- Tablas de frecuencias
8.- Tablas por intervalo de clases
9.- Tablas de doble entrada
10.- Representación gráfica de los datos
Competencia específica
Utilizaras las técnicas de representación numérica y gráfica para representar información a través de la organización de los datos obtenidos de una muestra o población.
2.1.Organización de datos y distribución de frecuencias
Introducción
La descripción estadística organiza los datos y los presenta en forma de tablas y gráficas. Esta área sólo describe, resume, organiza y representa los datos obtenidos de una población o muestra de la población, sin elaborar inferencias ni obtener conclusiones.
La organización de datos se realiza a través de tablas que se utilizan para simplificar la presentación y distribución de estos datos.
A continuación, conocerás que existen diferentes tipos de presentación de datos y con base en ellos, distintas clasificaciones de frecuencia, como: frecuencia relativa, frecuencia acumulada y frecuencia absoluta.
Definición de datos
agrupados y no agrupados
Los datos agrupados y no agrupados o series agrupadas y no agrupadas (que es lo mismo) se refiere al hecho de que están ordenados, clasificados y contados, por ejemplo
2,2,1,3,3,3,4,4,5,6,1,2,2,3,3,3,4,4,3
(Total 20 niños)
Estos son datos no agrupados por que
no los has clasificado y contado
1,1,2,2,2,2,3,3,3,3,3,3,3,4,4,4,4,5,5
(Total 20 niños)
Los datos no agrupados también los
puedes ordenar, por ejemplo de la edad menor a la edad
mayor, no están contabilizados ni clasificados solamente
están ordenados
1 Datos Agrupados
Las
características de los elementos de una población pueden
ser de tipo cualitativo o de tipo cuantitativo. En el
primero caso se trata de cualidades que distinguen un
elemento de otro y lo ubican en clases independientes y
separadas.
Las propiedades de tipo cuantitativo son aquellas que pueden medirse o contarse.
2.1.1. Frecuencias
Antes de comenzar con el tema, es importante que consideres lo siguiente:

Las cuatro formas de la frecuencia son:
Frecuencia o Frecuencia absoluta
Frecuencia absoluta acumulada
Frecuencia relativa.
Fecuencia relativa Absoluta
La frecuencia o
frecuencia absoluta es
el número de veces que se repite un valor dentro de un
conjunto de datos, se denota como fi.
Por ejemplo, supongamos que tienes la siguiente serie de datos: 3, 2, 5, 7, 3, 7, 7, 5, 2, 7, 3.
Si los organizas en una tabla, tendrás:
|
Dato |
Frecuencia |
|
2 |
2 (porque se repite 2 veces) |
|
3 |
3 (porque se repite 3 veces) |
|
5 |
2 (porque se repite 2 veces) |
|
7 |
4 (porque se repite 4 veces) |
|
Total de datos (N) |
11 |
Frecuencia absoluta acumulada
La
frecuencia absoluta acumulada es la suma
de las frecuencias de las variables hasta el renglón i,
se representa como Fi. También es
conocida como frecuencia acumulada. Siguiendo con el ejemplo
anterior:
|
Dato |
Frecuencia |
Frecuencia acumulada |
|
2 |
2 |
2 (hasta aquí tienes 2 datos) |
|
3 |
3 |
5 (la suma de la frecuencia del primer dato con la del segundo dato 2+3) |
|
5 |
2 |
7 (frecuencia de 2+frecuencia de 3+frecuencia de 5) |
|
7 |
4 |
11 (frecuencia de 2+frecuencia de 3+frecuencia de 5 frecuencia de 7) |
|
Total de datos (N) |
11 |
|
Frecuencia relativa
La frecuencia relativa es el resultado de dividir la frecuencia de cada dato entre el número total de datosuma de esta columna da 1 (excepto cuando el resultado de las divisiones se redondea). Este dato también puede verse como un porcentaje, se representa como hi. Siguiendo con el ejemplo anterior:
|
Dato |
Frecuencia |
Frecuencia acumulada |
Frecuencia relativa |
|
2 |
2 |
2 |
0.181 (se divide 2/11) |
|
3 |
3 |
5 |
0.272 (se divide 3/11) |
|
4 |
2 |
7 |
0.181 (se divide 2/11) |
|
5 |
4 |
11 |
0.363 (se divide 4/11) |
|
Total de datos (N) |
11 |
|
|
Frecuencia Relativa Acumulada
La frecuencia relativa acumulada es la suma de las frecuencias relativas hasta el renglón i. Se representa como Hi, observa el ejemplo:
|
Dato |
Frecuencia |
Frecuencia acumulada |
Frecuencia relativa |
Frecuencia relativa acumulada |
|
2 |
2 |
2 |
0.1818 |
0.1818 (hasta este renglón sólo tienes esta frecuencia relativa) |
|
3 |
3 |
5 |
0.2727 |
0.4545 (se suma la frecuencia relativa del primer dato con la del segundo dato 0.1818+0.2727) |
|
5 |
2 |
7 |
0.1818 |
0.6363 (la frecuencia relativa de 2+la frecuencia relativa de 3+la frecuencia relativa de 5) |
|
7 |
4 |
11 |
0.3636 |
0.9999 (la frecuencia relativa de 2+la frecuencia relativa de 3+la frecuencia relativa de 5+la frecuencia relativa de 7) |
|
Total de datos (N) |
11 |
|
|
|
Ejemplo de organización de frecuencias
A continuación observarás una tabla con la organización de frecuencias, los datos presentados son los siguientes números:
|
18, 41, 23, 47,18, 23, 23, 41, 41, 47, 47, 52, 23, 47, 23, 47, 18, 47, 7, 23, 18, 47, 52, 41, 52, 18, 23, 52, 7, 18, 52, 23. |
|
No. renglón |
Datos obtenidos de la variable |
Frecuencia fi |
Frecuencia |
Otra forma para obtenerFi |
Frecuencia relativa hi |
Frecuencia relativa acumulada Hi |
|
1 |
7 |
f1= 2 |
f1=F1= 2 |
f1 = F1=2 |
h1=f1/N=0.0625 |
h1= H1=0.0625 |
|
2 |
18 |
f2= 6 |
f1+f2= F2= 8 |
F1+f2=F2=8 |
h2=f2/N=0.1875 |
h1+h2= H2= |
|
3 |
23 |
f3= 8 |
f1+f2+f3= F3=16 |
F2+f3=F3=16 |
h3=f3/N=0.2500 |
h1+h2+h3= |
|
4 |
41 |
f4= 4 |
f1+f2+f3+f4=F4=20 |
F3+f4=F4=20 |
h4=f4/N=0.1250 |
h1+h2+h3+h4 |
|
5 |
47 |
f5= 7 |
f1+f2+f3+f4+f5=F5=27 |
F4+f5=F5=27 |
h5=f5/N=0.2187 |
h1+h2+h3+ |
|
6 |
52 |
f6= 5 |
f1+f2+f3+f4+f5+f6=F6=32 |
F5+f6=F6=32 |
h6=f6/N=0.1563 |
h1+h2+h3+ |
|
Total |
|
N=32 |
|
|
1.0000 |
|
Ejercicio sugerido para trabajar con excel
Tomando los datos obtenidos del conteo de color de autos como ejemplo deberas de cambiar los datos de la hoja con tus datos, revisa el siguiente documento: Autos_colores.
Ejemplo de frecuencias con Medidas de tornillos
Frecuencias
Revisa este libro de Excel y realiza tus comentarios de este.
Para complementar esta lectura revisa o descarga el siguiente documento Frecuencias realiza los ejemplos presentados ahi.2.1.2. Intervalos
Otro concepto muy utilizado en estadística descriptiva es el de intervalo. Conoce qué es y los demás conceptos asociados.
Intervalos
**************************************************************************************************************Conjunto de valores agrupados entre dos números, conocidos como límites, en este caso, límites del intervalo.
*****************************************************************************************
Intervalo de clase
**********************************************************
Se llama intervalo de clase a la expresión que denota un intervalo.
***********************************************************************Amplitud del intervalo
***********************************************************************************************La
amplitud del intervalo es la distancia que hay entre los
límites superior e inferior del intervalo.
Se calcula restando el valor del límite inferior al valor del límite superior.
************************************************************************************************Frontera de clase
**************************************************************************************************************************Son los puntos medios entre los límites de intervalos consecutivos. Las fronteras de clase se utilizan para recuperar los datos entre el límite superior de un intervalo y el límite inferior del siguiente.
********************************************************************************************************************************
Marca de clase
*******************************************************************************************************************************También conocida como punto medio de clase, es el resultado de la suma de los límites inferior y superior del intervalo, dividido entre dos.
*********************************************************************************************************************************Ejemplo de intervalos
Observa cómo se representan los conceptos relacionados con los intervalos.
Dados
los números 15 y 25, tendráas que:
El intervalo corresponde
a todos los números que se encuentran entre 15 y 25.
El intervalo de clase sería: 15-25
Los límites del intervalo son:
Lmite inferior=15
Límite superior=25
La amplitud del intervalo
15-25 sería: 25 menos 15, es decir, 10.
Es recomendable que todos los intervalos tengan la misma amplitud, por lo que se puede restar el dato menor al dato mayor y dividir el resultado entre el número de intervalos.
La frontera de clase: dados los intervalos 4-14, 15-25 y 26-36, las fronteras de clase serían: 3.5 y 14.5, para el primer intervalo, 14.5 y 25.5 para el segundo intervalo, por último, 25.5 y 36.5 para el tercer intervalo.
La marca de clase del intervalo 15-25 es igual a: 15+25=40/2=20.
Es recomendable que la marca del intervalo coincida con alguno de los datos, aunque esto no es necesario ni siempre se logra; sobre todo cuando los intervalos tienen la misma amplitud.
2.1.3. Construcción de intervalos de clase
La formación de clases o intervalos de clase, que se representa con (k), dependen, generalmente, del tamaño del rango de la población o muestra. Lo que se debe hacer para determinar los intervalos de clase es lo siguiente.
Paso 1. Calcular el rango
Se identifica el número mayor (Xn) y el número menor (X1) en los datos. El rango es el resultado de restar el número menor al número mayor; esto es:
R= Xn >
X1
Por ejemplo:
Para una serie de datos que van desde el 18 hasta el 56,se tiene lo siguiente:
Xn= 56
X1= 18
por lo tanto, R= Xn - X1= 56 - 18= 38
Paso 2. Determinar el número de intervalos que se desea tener
No existe una regla para determinar el número de intervalos, pero generalmente se suelen crear entre 5 y 20 intervalos. La decisión la toma el investigador. siguiendo con el ejemplo, se van a construir 7 intervalos. Entonces k= 7
Paso 3. Dividir el rango entre el número de intervalos que se desea tener
Recuerda que es recomendable elegir un número entre 5 y 20 para los intervalos y dividir el rango entre el número deseado de intervalos.
Siguiendo con el ejemplo:
Si son 7 intervalos 38/7 = 5.428
Esta será la amplitud de los intervalos. Cuando no es un número entero, se escoge el entero sin decimales.
Paso 4. Formación de intervalos:
Los intervalos se forman comenzando un número antes del primer dato. x1-1
Intervalos:
17 a
22 (se cuenta 5 desde 18 hasta 22)
23 a 28 (el siguiente intervalo comienza a partir del límite
superior del intervalo anterior)
29 a 34
35 a 40
41 a 46
47 a 52
53 a 58
Ejemplo de construcción de intervalos
El director de una consultoría en desarrollo de software desea conocer el número de incidencias en sus desarrollos reportadas durante los meses de agosto y septiembre. Para ello registra los siguientes datos:
35, 24, 26, 23, 50, 20, 25, 56, 30, 30, 38, 36, 35, 29, 28, 30, 40, 39, 38, 40, 27, 24, 30, 32, 35, 27, 29, 22, 28, 27, 48, 40, 48, 31, 39, 28, 46, 36, 37, 52, 44, 49, 52, 41, 31, 31, 56, 58, 38, 26, 25, 24, 60, 55, 48, 37, 31, 30, 22, 20.
Observa cada paso:
1.-Calcular el rango: R=Xn-X1=60-20=40
2.-Determinar el número de intervalos entre 5 y 20:Elegir
8
intervalos.
3.-Dividir el rango entre el número de
intervalos:40/8=5
4.-Se forman los intervalos:Comenzar
por un número anterior al límite inferior: 19-24, 25-30,
31-36, 37-42, 43-48, 49-54, 55-60
Actividad 3: Intervalos
Descarga el archivo Intervalos y analiza los datos y formulas que se presentan ahi, y cambia los datos por datos de los tornillos.
Existen diferentes tipos de tablas para presentar datos, las más utilizadas son: Tabla de datos, Tabla de frecuencias, Tabla por intervalos de clase y Tablas de doble entrada. Conoce en qué consiste cada una:
Tablas de datos
Una
tabla de datos es la forma más sencilla de organizar un
conjunto de datos y se utiliza cuando la información que
necesitas son los datos mismos. (para presentar estas
tablas en excel revise este tema formatos en excel en el
titulo Tablas de Datos)
Se organizan en columnas o renglones y se registran las mediciones o datos obtenidos.
Ejemplo:
Imagina que la medición de temperatura a lo largo del día da como resultado los siguientes valores (en grados Celsius): 20.4, 21.2, 22.1, 23.9, 25.3, 26.9, 27.7
A partir de estos valores construyes la siguiente tabla:

Las tablas de frecuencia aportan mayor información que las tablas de datos, ya que están construidas con las categorías de la variable que se está midiendo y su frecuencia.
Ejemplo:
Un
experimento da como resultado los siguientes valores:
1, 2, 2, 2, 1, 1, 5, 4, 3, 2, 2, 1, 3, 4, 5, 6, 2, 3, 4, 5, 5,
4, 3, 3, 2
Si agrupas los datos por categorías, según la frecuencia o número de veces que aparece cada dato, tendrás la siguiente tabla:

Las
tablas de frecuencias pueden construirse anexando las columnas
correspondientes a la frecuencia acumulada, la frecuencia
relativa y frecuencia relativa acumulada.
Revisa
esta
hoja de trabajo en excel donde se puede aprobechar las
diferentes funciones en Excel usando las tablas dinamicas,
combinandolos con la estadística frecuencias_y_tablas_dinamicas
si no conoces como funcionan las tablas dinamicas revisa
esto: tablas dinamicas
revisa el titulo tablas dianmicas y realiza los ejercicios
que se presentan.
2.1.6. Tablas por intervalos de clase
En este tipo de tablas los datos son presentados por intervalos de clase y no por los valores correspondientes a cada variable.
Ejemplo: En una encuesta sobre el desempleo en el área metropolitana de la ciudad de México, se organizan los datos por grupos de edades (intervalos de clase) y se presenta la frecuencia de cada intervalo, teniendo un total de 23,700 desempleados.
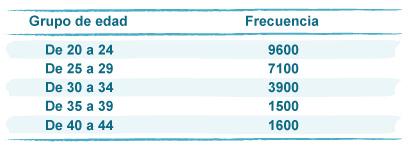
2.1.7. Tablas de doble entrada
Estas tablas proporcionan información referente a dos variables o eventos relacionados entre sí. La información se distribuye poniendo en los renglones de la tabla la información de una de las variables y en las columnas la información de la otra variable.
Ejemplo: Se cuenta el número de cirugías realizadas por edades en una muestra de 100 personas, los resultados son los siguientes:
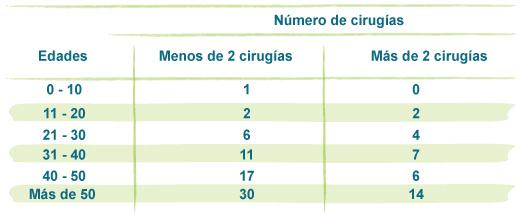
Una tabla cualquiera puede ser vista como una tabla de doble entrada, en la cual las variables relacionadas son los rangos contra el valor de las variables en dicho rango. Por ejemplo, imagina que mides la temperatura de un líquido con respecto al tiempo de calentamiento. En el renglón colocas los tiempos y en las columnas la temperatura obtenida. Puedes considerar la tabla como una tabla de frecuencias o como una tabla de doble entrada:

2.2. Representación gráfica de los datos
El tema anterior presentá diferentes formas de organizar o de tabular datos y la distribución de frecuencias. Ahora estudiarás la representación gráfica de los datos.
Las gráficas son representaciones visuales de los datos que se muestran en una tabla. Existen diferentes tipos de gráficas, cada una de ellas se elabora con base en el tipo de información que se quiere representar.
El histograma es la representación gráfica de una variable continua. Se elabora en un sistema de coordenadas rectangulares. El eje horizontal se utiliza para representar la variable independiente, es decir, la escala de medición o fronteras de clase. El eje vertical representa la escala de frecuencias. Si los intervalos de clase tienen el mismo ancho, las alturas de las barras serán proporcionales a las frecuencias.
Si se desea hacer un repaso de la graficación en Excel revise el siguiente enlace de gráficas en Excel
El histograma permite apreciar visualmente la distribución y dispersión de las mediciones

2.2.2. Gráfica de barras
Este
tipo de gráfica se utiliza para datos de tipo ordinal,
nominal y discreto. En éstas se muestran la frecuencia,
la frecuencia relativa y el porcentaje por medio de la altura
y no por el área de la barra. Esta gráfica
muestra las discontinuidades en las mediciones por medio de
espacios vacíos entre las barras.
La gráfica de barras se traza sobre un eje de coordenadas. Y puede ser de dos formas:
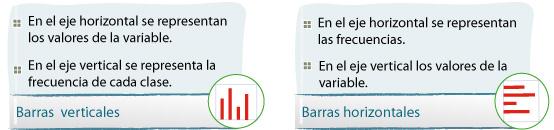
Un
histograma y una gráfica de barras son muy semejantes, la
diferencia radica en que el histograma no presenta separación
entre las barras. (un grafico de barras se puede pasa a
histograma ensanchando las barras revisa este documento para
graficos estadísticos Gráficos)
2.2.3. Gráfica de líneas
Una gráfica de
líneas también se construye en un sistema coordenado
rectangular y muestra la relación entre las variables
mediante puntos conectados por líneas continuas. La
frecuencia de cada valor medido es representada por la altura
del punto.
En el eje horizontal se representa la variable y en el eje vertical, la frecuencia. Se determinan los puntos de corte del valor de la variable con su frecuencia y se unen, obteniéndose la gráfica de línea.
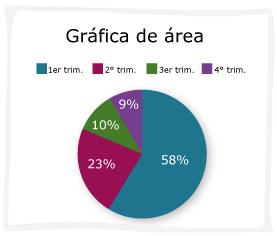
2.2.4. Gráfica de áreas o de pastel
Una forma de representar datos u observaciones de una variable cualitativa es mediante un diagrama circular. Esta gráfica muestra la relación entre las variables dividiendo un círculo (o pastel) en sectores (o rebanadas). También, se utilizan para representar la distribución de frecuencias, pero es el área de cada sector la proporcional a los valores medidos.
Para trazar la gráfica, se hace una distribución proporcional de las frecuencias del problema con respecto a la circunferencia, determinando sectores circulares para cada categoría.




Los parámetros que has visto hasta aquí, la organización numérica de los datos en tablas y las representaciones gráficas de éstas, pueden ser realizados de forma manual, pero existen programas informáticos como Excel, y de software libre y programas especializados para estadástica, que permiten realizar todos estos trabajos.
Realiza la siguiente actividad:
1.Retoma los problemas que realizaste anteriormente: Frecuencias, con los datos de la tabla elabora las gráficas que revisaste en este tema e inclúyelas.