
CE.CA.T.I. No. 89; Celaya, Gto.
(Secretaría de Educación Pública)

Medidas
de
tendencia central y dispresión
Para cualquier conjunto de datos estudiados es importante tener un resumen de la información y sus características. Esta información indica cómo se comporta la población de datos que tienes. Para resumir la información se utilizan dos tipos de valores que, en vez de representar cada uno de los datos, representan conjuntos de datos. Estos dos tipos de indicadores estadísticos son: las medidas de tendencia central, que muestran hacia qué valores se agrupan o acumulan los datos; y las medidas de dispersión, que de forma contraria a las anteriores, muestran cómo se dispersan o separan los datos.
Propósito
de
la unidad
En esta unidad:
Aplicarás el procedimiento para obtener las medidas de tendencia central y dispersión en datos agrupados y no agrupados.
Utiliza
las medidas de tendencia central y dispersión para describir un
conjunto de datos mediante la representación numérica y gráfica
de la información obtenida en una muestra o población.
Antes
de proceder revise lo siguiente: Medidas
de tendencia Central revisa las 3 primeras hojas
regresaremos a revisar los ejercicios posteriormente
3.1. Medidas de tendencia
central
Las
medidas de tendencia central son los valores que representan un
conjunto de datos de forma tal que te ayudan a saber dónde están acumulados los datos
sin indicar cómo se distribuyen. Se llaman así porque tienden a
ubicarse en la parte central del conjunto de datos. Las medidas
de tendencia central más comunes son: la media aritmética
(conocida como media o promedio), la mediana y la moda.
Media aritmética
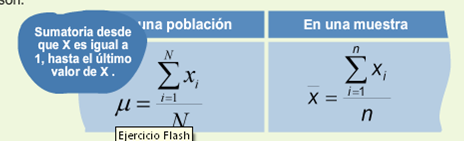
La media aritmética o, simplemente, media, se denota por x la letra μ (letra griega) según se calcule en una muestra o en la población, respectivamente. La media es resultado de dividir la suma de todos los valores de los datos entre el número total de datos.
La manera como se organizan los datos: no agrupados y agrupados (por frecuencias o intervalos), determina la expresión de la fórmula para calcular la media.

Fórmula para datos no agrupados
Los datos no agrupados son aquellos datos que se organizan en una tabla de datos, es decir, cada valor se representa de manera individual. Las fórmulas para calcular la media son:
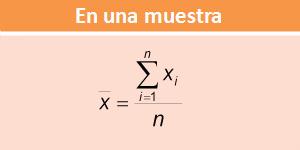 |
 |


En una muestra
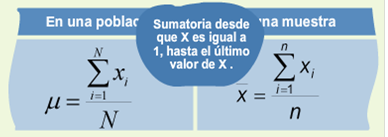

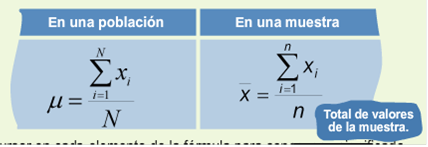
En estas fórmulas la diferencia radica en que, el total de la población se representa con la letra N y el total de la muestra se representa con la letra n.
Media
aritmética
Fórmula para datos agrupados en frecuencias
Los datos agrupados en frecuencias son aquellos que se organizan en una tabla de frecuencias, es decir, las tablas que contienen, en una columna, el valor de la variable y, en otra columna, la frecuencia o el número de veces que se repite cada valor en una serie de datos.
Las fórmulas para calcular la media con los datos organizados de esta manera son:
 |
 |

En una muestra

Media aritmética
Fórmula para datos agrupados en intervalos
Los datos agrupados en intervalos son los que se organizan dentro de un rango establecido entre un límite inferior y un límite superior. Recuerda que las tablas de intervalos muestran el número de datos que abarca cada intervalo (frecuencia por intervalo). Las fórmulas para calcular la media con los datos organizados de esta manera son:
 |
 |



En una muestra



Ejercicio para
media aritmetica no agrupados y poblacion.
|
Los suguientes documentos te ayudarán a comprender cómo se usan las fórmulas, da clic en los links para revisarlos.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Con los datos de este problema, tendrás que obtener las medidas de tendencia central y dispersión, por lo tanto, esta actividad está dividida en seis momentos.
Es importante que la actividad la realices paso a paso, ya que si tienes dudas sobre el uso de las fórmulas, puedes consultarlas a tiempo con tu Instructor; además, tendrás que entregar tu trabajo al final del tema.
Analiza el problema y selecciona la fórmula adecuada para obtener la media aritmética.
No olvides incluir la fórmula y las operaciones que realices.
Mediana
La segunda medida de tendencia central es la mediana, esta se define como:
|
El valor que divide en dos partes iguales una serie de datos, es decir, la cantidad de datos que quedan a la derecha de la mediana es igual a la cantidad de datos que quedan a la izquierda. Se representa por Me. |
Para calcular la mediana, debes hacer lo siguiente:
Para
cuando la cantidad de valores es impar
Ordena los valores de menor a mayor y busca el valor del centro.
Por ejemplo:
1.- Supón
que tienes los siguientes valores:
2, 4, 0, 8, 6, 4, 7, 1, 1, 0, 8, 6, 9
2.-
Ordena:
0, 0, 1, 1, 2, 4, 4, 6,
6, 7, 8, 8, 9
3.- El dato
que divide a la mitad es:
4.- por lo tanto Me: 4
Para cuando la cantidad de valores es par
Ordena los
valores de menor a mayor,busca y promedia los
valores del centro.
Por ejemplo:
1.- Supón
que tienes los siguientes valores:
5, 7, 2, 3, 1, 6, 9, 8, 6, 4, 7, 1 ,3, 2
2.- Ordena:
1, 1, 2, 2, 3, 3, 4, 5, 6,
6, 7, 7, 8, 9
3.- Busca y promedia los datos del centro:
4.- 4+5=9/2= 4.5, por lo tanto Me: 4.5
Mediana en datos agrupados por intervalos
Cuando
quieres calcular la mediana en datos agrupados por intervalos, tienes que buscar el
intervalo donde la frecuencia acumulada llega hasta la mitad de
la suma de las frecuencias absolutas, es decir, es necesario
localizar el intervalo donde se encuentre N/2, para ello utiliza
la siguiente fórmula:
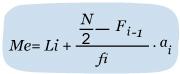

Lee el documento Mediana por intervalos.
Actividad 2: Medidas de tendencia central. Mediana
3.1.3. Moda
La
tercera medida de tendencia central es la moda.
|
La moda es el valor que tiene mayor frecuencia absoluta, es decir, el valor que se repite más veces en una serie de datos. La moda se denota por Mo. |
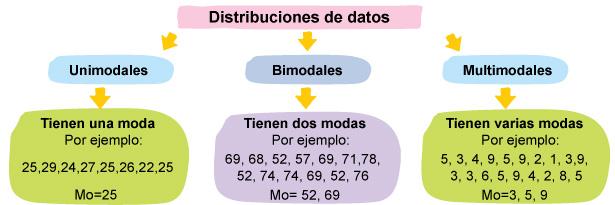
Cuando todos los valores de la distribución de datos tienen igual número de frecuencia, se dice que no hay moda.
Moda en datos agrupados por intervalos
Cuando la distribución de datos es por intervalos de clase, primero se localiza el intervalo que tiene mayor frecuencia absoluta utilizando la siguiente fórmula para calcular la moda:
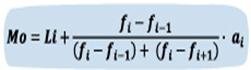
Donde:
Li es el límite inferior del intervalo modal.
fi es la frecuencia absoluta del intervalo modal.
fi-1 es la frecuencia absoluta del intervalo anterior al intervalo modal.
fi+1 es la frecuencia absoluta del intervalo siguiente al intervalo modal.
ai es la amplitud del intervalo.
Lee el documento Moda por intervalos de clase.
Actividad 3: Medidas de tendencia central. Moda
Calcula la moda en el problema Frecuencias. Recuerda que ya debiste haber obtenido la media y la mediana.
A diferencia de las medidas de tendencia central, que miden acumulaciones en un solo punto, las medidas de dispersión miden el grado de separación o alejamiento que tiene una variable estadística con respecto a una medida de posición o tendencia central. Dicho grado de separación indica lo representativa que es la medida de posición con respecto al conjunto total de datos. A mayor dispersión, menor representatividad de la medida de posición y viceversa.
3.2.1.
Recorrido
El
recorrido representa la diferencia que hay entre el primero y el
último valor de la variable, tambiérn se le conoce como rango y
se denota por Re.
La fórmula para calcularlo es:
![]()
|
Donde: |
máx xi es el valor
máximo de la variable |
Por ejemplo:
Si tienes la siguiente distribución de datos: 69, 68, 52, 57, 69, 71, 78, 52, 74, 74, 69, 52, 76, calcula el rango, sustituyendo los valores Re=78-52=26
Las actividades de este tema se desarrollarón de manera similar que las actividades del tema anterior. En esta actividad también está disponible un espacio para que plantees tus dudas sobre le tema y el uso de las fórmulas, este foro se titula Medidas de dispersión.
1.Con los datos del problema Frecuencias (el cual trabajaste en actividades anteriores), calcula el recorrido de la distribución.
La varianza mide la mayor o menor dispersión de los valores de la variable respecto a la media aritmética. Siempre es mayor o igual que cero y menor que infinito. Se define como la media de los cuadrados de las diferencias del valor de los datos menos la media aritmética de éstos.
La fórmula de la varianza para datos no agrupados es:
|
Para calcularla en una población: en excel =varp(rango) |
|
Donde |
|
es la suma de los cuadrados de los valores de X menos la media |
|
|
|
|
|
|
|
Para calcularla en una muestra: en excel =vara(rango) |
|
N, n |
es el número total de datos. |
|
|
|
||||
Varianza para datos agrupados por intervalos
La fórmula para calcular la varianza en datos agrupados por intervalos es la siguiente:
La
fórmula para calcular la varianza en datos agrupados por
intervalos es la siguiente:
|
Para calcularla en una población: |
|
Donde: |
Fi |
es la frecuencia del intervalo. |
|
Mci |
es la marca de clase del intervalo. |
|||
|
Para calcularla en una muestra: |
|
|
es la media de la distribución de datos. |
|
|
N, n |
es el número total de datos de la distribución |
Para ver un ejemplo, lee el documento Varianza en datos agrupados por intervalos.
Ya que obtuviste el recorrido de la distribución de datos del problema Frecuencias, calcula la varianza, incluyendo la fórmula y las operaciones.
La desviación típica o estándar muestra qué tan alejado está un dato del valor de la media aritmítica, es decir, la diferencia que hay entre un dato y la media aritmética.
Se denota como S o σ según se calcule en una muestra o en toda la población, respectivamente.
Se define como la raíz cuadrada positiva de la varianza. Se expresa mediante las siguientes fórmulas:
En datos no agrupados
Para una población |
Para una muestra |
|
|
|
En datos agrupados agrupados por intervalos |
|
Para una población
|
Para una muestra
|
|
|
|
Con los datos de la varianza que obtuviste en la actividad anterior, calcula la desviación típica en el mismo problema.
Realiza los mismos ejercicios del tema medidas de tendencia central
Revisa
y Realiza los ejemplos del tema de Medidas
de dispersion